题目内容
6.将二次函数y=x2-2x+3化为y=a(x+h)2+k的形式,结果为( )| A. | y=(x+1)2+2 | B. | y=(x-1)2+4 | C. | y=(x+1)2+4 | D. | y=(x-1)2+2 |
分析 利用配方法求解.
解答 解:y=x2-2x+3=x2-2x+1+2=(x-1)2+2
故选D.
点评 本题考查了二次函数的三种形式:一般式:y=ax2+bx+c(a,b,c是常数,a≠0);顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k);交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(x2,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
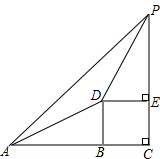 山顶上有一个电视铁塔,从地面A点看铁塔顶P的仰角是45°,沿坡度i=1:$\sqrt{3}$的山坡向 上走了100米,到达D点,再看铁塔顶P的仰角是60°,求铁塔顶P到地面的距离PC(结果保留根号).
山顶上有一个电视铁塔,从地面A点看铁塔顶P的仰角是45°,沿坡度i=1:$\sqrt{3}$的山坡向 上走了100米,到达D点,再看铁塔顶P的仰角是60°,求铁塔顶P到地面的距离PC(结果保留根号).