��Ŀ����
1��If we let��a��be the greatest prime number not more than a then the result of the expression����3������25������30����is��������������壼a��Ϊ������a�������������3������25������30������ֵΪ��������
| A�� | 1333 | B�� | 1999 | C�� | 2001 | D�� | 2249 |
���� ���ݣ�a��Ϊ������a������������ɵ���Ӧ�������������������ij˷����ɵû����ٸ��ݣ�a��Ϊ������a������������ɵô𰸣�
��� �⣺����3������25������30����=��3��23��29��=��2001��=1999��
��ѡ��B��
���� ���⿼������������������ã�a��Ϊ������a����������ó���Ӧ����������ǽ���ؼ���ע�ⲻ����2001�����������1999��

��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
�����Ŀ
13��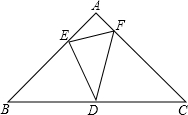 ��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ�
��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ�
�ٵ�BE=1ʱ��S��CDF=$\frac{\sqrt{2}}{2}$���ڡ�DFC=��EDB����CF•BE=1����C��AEF=$\sqrt{2}$����S��AEF+2S��DEF=$\frac{1}{2}$��
��ȷ���У�������
 ��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ�
��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ��ٵ�BE=1ʱ��S��CDF=$\frac{\sqrt{2}}{2}$���ڡ�DFC=��EDB����CF•BE=1����C��AEF=$\sqrt{2}$����S��AEF+2S��DEF=$\frac{1}{2}$��
��ȷ���У�������
| A�� | �٢ڢ� | B�� | �٢ۢܢ� | C�� | �ڢۢ� | D�� | �ۢܢ� |
11��������y=ax2+bx+3��a��0����A��4��4����B��2��m�����㣬��B�������߶Գ���ľ����Ϊd������0��d��1����ʵ��m��ȡֵ��Χ�ǣ�������
| A�� | m��2��m��3 | B�� | m��3��m��4 | C�� | 2��m��3 | D�� | 3��m��4 |
 ��ͼ��AD�ǡ�ABC�ĸߣ�BEƽ�֡�ABC��AD��E������C=62�㣬��BED=66�㣬���BAC�Ķ�����
��ͼ��AD�ǡ�ABC�ĸߣ�BEƽ�֡�ABC��AD��E������C=62�㣬��BED=66�㣬���BAC�Ķ�����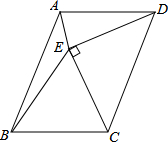 ��ͼ��?ABCD�ı�CDΪб������������ֱ�ǡ�CDE��ʹAD=DE=CE����DEC=90�㣬�ҵ�E��ƽ���ı����ڲ�������AE��BE�����AEB�Ķ�����
��ͼ��?ABCD�ı�CDΪб������������ֱ�ǡ�CDE��ʹAD=DE=CE����DEC=90�㣬�ҵ�E��ƽ���ı����ڲ�������AE��BE�����AEB�Ķ�����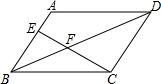 ��ͼ����?ABCD�У�E��AB���ϵ�һ�㣬����CE���Խ���BD��F����AE��BE=2��3�����BEF�͡�DCF���ܳ�֮��Ϊ3��5��
��ͼ����?ABCD�У�E��AB���ϵ�һ�㣬����CE���Խ���BD��F����AE��BE=2��3�����BEF�͡�DCF���ܳ�֮��Ϊ3��5��