题目内容
2.若3n=2,3m=5,则32n+m-1=$\frac{20}{3}$.分析 根据幂的乘方,可得同底数幂的乘除法,根据同底数幂的乘除法,可得答案.
解答 解:32n=(3n)2=4,
32n+m-1=32n×3m÷3=4×5÷3=$\frac{20}{3}$.
故答案为:$\frac{20}{3}$.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.

练习册系列答案
相关题目
7.如果(x2+px+q)(x2+7)的展开式中不含x2与x3的项,那以p,q的值是( )
| A. | p=1,q=7 | B. | p=0,q=-7 | C. | p=2,q=1 | D. | p=0,q=7 |
12.已知关于x的一元二次方程a(1+x2)+2bx=c(1-x2),其中a、b、c分别为△ABC三边的长,如果方程有两个相等的实数根,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
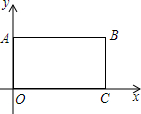 如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过y=ax2+bx+c(a≠0)点A.
如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过y=ax2+bx+c(a≠0)点A.
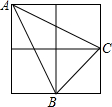 如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.
如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中AB边上的高是$\frac{3\sqrt{5}}{5}$.