题目内容
12．对于实数a、b，定义运算某“*”：a*b=$\left\{\begin{array}{l}{{a}^{2}-ab（a≥b）}\\{ab-{b}^{2}（a＜b）}\end{array}\right.$．例如4*2，因为4＞2，所以4*2=42-4×2=8．若x1、x2是一元二次方程x2-4x+3=0的两个根，则x1*x2=2或6．分析 直接利用十字相乘法分解因式解方程，再利用已知定义得出答案．
解答 解：∵x1、x2是一元二次方程x2-4x+3=0的两个根，
∴（x-3）（x-1）=0，
解得：x1=1，x2=3，
∵1＜3，
∴x1*x2=1×3-32=-6，
当x1=3，x2=1，
∵3＞1，
∴x1*x2=32-1×3=6，
故答案为：-6或6．
点评 此题主要考查了因式分解法以及新定义，正确分解因式是解题关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
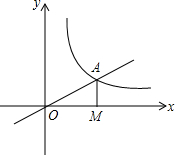如图，正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知△OAM的面积为1．如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．
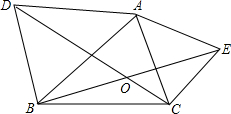已知，如图，AB=AD，AC=AE，∠DAB=∠CAE=50°．
