题目内容
20.先化简,再求值:$\frac{{x}^{2}-2x+1}{{x}^{2}+2x}$÷$\frac{1-{x}^{2}}{x+2}$+$\frac{1}{x+1}$,其中x的值从不等式组$\left\{\begin{array}{l}{2(x+3)≥3-x}\\{3-\frac{x+1}{4}>2}\end{array}\right.$的整数解中取一个使原式有意义的值代入计算求值.分析 先根据分式混合运算的法则把原式进行化简,再求出不等式组的解集,选取合适的x的值代入进行计算即可.
解答 解:原式=$\frac{(x-1)^{2}}{x(x+2)}×\frac{x+2}{-(x+1)(x-1)}+\frac{1}{x+1}$
=-$\frac{x-1}{x(x+1)}+\frac{x}{x(x+1)}$
=$\frac{1}{x(x+1)}$,
解不等式组$\left\{\begin{array}{l}{2(x+3)≥3-x}\\{3-\frac{x+1}{4}>2}\end{array}\right.$得:-1<x<3,
当x=2时,原式=$\frac{1}{2×3}$=$\frac{1}{6}$.
点评 本题综合考查了分式的化简与一元一次不等式组的整数解.解这类题的关键是利用分解因式的方法化简分式,并会求不等式组的整数解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.2011年9月1日起我国施行了新的《中华人民共和国个人所得税法》,与以前的法案相比较,新的法案部分内容修改后,可理解为:
①工资、薪金所得总和减去3500元后的余额为全月应纳税所得额.
②个人所得税税率表(工资、薪金所得适用)修改为:
如某人某月工资4000元,则其该月应纳税所得额为4000-3500=500(元),应缴个人所得税500×3%=15(元)
请你根据以上的信息解答下列问题:
(1)某一大型私营公司员工全月应纳税所得额为x元,用x的代数式分别表示:①当0<x≤1500 时,个人所需缴纳的所得税是3%x元
②当1500<x≤4500时,个人所需缴纳的所得税是(0.1x-105)元
(2)这家公司的某位员工在十一月份得工资6800元,求出他应缴纳的个人所得税是多少元?
(3)如果这家公司某个部门的经理在某一个月缴纳了个人所得税295元,求出该经理在这个月的工资收入是多少元?
①工资、薪金所得总和减去3500元后的余额为全月应纳税所得额.
②个人所得税税率表(工资、薪金所得适用)修改为:
| 级数 | 全月应纳税所得额 | 税率% |
| 一 | 不超过1500元的 | 3 |
| 二 | 超过1500元至4500元的部分 | 10 |
| 三 | 超过4500元至9000元的部分 | 20 |
| 四 | 超过9000元至35000元的部分 | 25 |
| 五 | 超过35000元至55000元的部分 | 30 |
| 六 | 超过55000元至80000元的部分 | 35 |
| 七 | 超过80000元的部分 | 45 |
请你根据以上的信息解答下列问题:
(1)某一大型私营公司员工全月应纳税所得额为x元,用x的代数式分别表示:①当0<x≤1500 时,个人所需缴纳的所得税是3%x元
②当1500<x≤4500时,个人所需缴纳的所得税是(0.1x-105)元
(2)这家公司的某位员工在十一月份得工资6800元,求出他应缴纳的个人所得税是多少元?
(3)如果这家公司某个部门的经理在某一个月缴纳了个人所得税295元,求出该经理在这个月的工资收入是多少元?
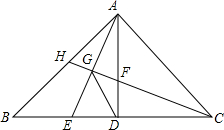 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.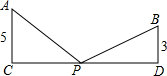 如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米?
如图,A、B两个工厂合用的一个变压器位于P处,两厂位于过P的笔直高压输电线的同一侧,P到A、B两厂的距离相等,A、B两厂到高压线的距离分别为AC、BD,且AC=5千米,BD=3千米.如果CD=16千米,那么变压器所在处P与C处的距离是多少千米? 如图,OC⊥AB于O,OD⊥OE于O,图中相等的角5对;互余的角有4对;互补的角有7对.
如图,OC⊥AB于O,OD⊥OE于O,图中相等的角5对;互余的角有4对;互补的角有7对.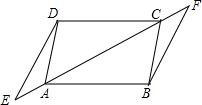 如图,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,试说明∠E=∠F.
如图,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,试说明∠E=∠F.