题目内容
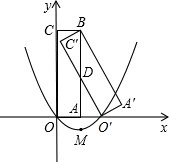 如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形.
如图,矩形O′A′BC′是矩形OABC绕点B逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3),顶点M的纵坐标为-1,求二次函数对称轴右侧的图象上点P,使得△POB是以OB为直角边的直角三角形.考点:矩形的性质,二次函数图象上点的坐标特征
专题:
分析:连接OB,根据旋转的性质可得OB=O′B,表示出点O′的坐标,然后求出抛物线顶点坐标,设抛物线解析式为y=a(x-1)2-1,利用待定系数法求出二次函数解析式,①把△AOB绕点O顺时针旋转90°求出B′的坐标,再求出OB′的解析式,与二次函数解析式联立求解即可得到点P的坐标,②把△AOB绕点B逆时针旋转90°得到点O′的坐标,再求出BO′的解析式,与二次函数解析式联立求解即可得到点P的坐标.
解答: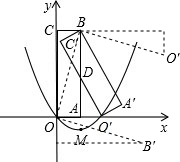 解:如图,连接OB,
解:如图,连接OB,
由旋转的性质得,OB=O′B,
∵B(1,3),
∴点O′(2,0),
∵顶点M的纵坐标为-1,
∴M(1,-1),
设抛物线解析式为y=a(x-1)2-1,
则a(2-1)2-1=0,
解得a=1,
所以,抛物线解析式为y=(x-1)2-1=x2-2x,
①把△AOB绕点O顺时针旋转90°得B′(3,-1)的坐标,
所以,直线OB′的解析式为y=-
x,
联立
,
解得
(舍去),
,
所以,点P的坐标为(
,-
),
②把△AOB绕点B逆时针旋转90°得到点O′(4,2),
设直线BO′的解析式为y=kx+b,
则
,
解得
,
所以,直线O′B的解析式为y=-
x+
,
联立
,
解得
,
(舍去),
所以,点P的坐标为(
,
),
综上所述,△POB是以OB为直角边的直角三角形时,P(
,-
)或(
,
).
 解:如图,连接OB,
解:如图,连接OB,由旋转的性质得,OB=O′B,
∵B(1,3),
∴点O′(2,0),
∵顶点M的纵坐标为-1,
∴M(1,-1),
设抛物线解析式为y=a(x-1)2-1,
则a(2-1)2-1=0,
解得a=1,
所以,抛物线解析式为y=(x-1)2-1=x2-2x,
①把△AOB绕点O顺时针旋转90°得B′(3,-1)的坐标,
所以,直线OB′的解析式为y=-
| 1 |
| 3 |
联立
|
解得
|
|
所以,点P的坐标为(
| 5 |
| 3 |
| 5 |
| 9 |
②把△AOB绕点B逆时针旋转90°得到点O′(4,2),
设直线BO′的解析式为y=kx+b,
则
|
解得
|
所以,直线O′B的解析式为y=-
| 1 |
| 3 |
| 10 |
| 3 |
联立
|
解得
|
|
所以,点P的坐标为(
5+
| ||
| 6 |
55-
| ||
| 18 |
综上所述,△POB是以OB为直角边的直角三角形时,P(
| 5 |
| 3 |
| 5 |
| 9 |
5+
| ||
| 6 |
55-
| ||
| 18 |
点评:本题考查了矩形的性质,二次函数图象上点的坐标特征,旋转的性质,利用旋转求出另一直角边所在的直线的解析式是解题的关键.

练习册系列答案
相关题目
下列各数
,0.31,
,
,
,0.90108,
中,无理数有( )
| 3 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 7 |
6+
|
| A、2个 | B、3个 | C、4个 | D、5个 |
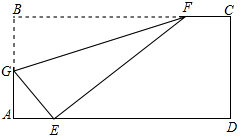 如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.
如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.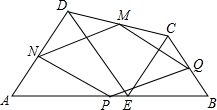 如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,
如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三角形,AB、BC、CD、DA的中点分别为P、Q、M、N,