题目内容
从1开始的自然数中,把能表示成两个整数的平方差的数从小到大排列成一列,则这列数中,第1998个数是 .
考点:规律型:数字的变化类
专题:
分析:首先将符合条件的整数分解成两整数的和与这两整数的差的积,再由整数的奇偶性,判断这个符合条件的整数,是奇数或是能被4整除的数,从而找出符合条件的整数的个数,每20个数中有5个4的倍数.
解答:解:对x=n2-m2=(n+m)(n-m)
(1≤m<n,m,n为整数)
因为n+m与n-m同奇同偶,所以x是奇数或是4的倍数,
+
=1998,
解得x=2664.
故答案为:2664.
(1≤m<n,m,n为整数)
因为n+m与n-m同奇同偶,所以x是奇数或是4的倍数,
| x |
| 2 |
| x |
| 4 |
解得x=2664.
故答案为:2664.
点评:本题考查了数字的变化类,通过观察、分析、归纳并发现其中的规律是解题关键.

练习册系列答案
相关题目
下列方程的变形中,正确的是( )
| A、由2=3-x,得x=2+3 | ||||
| B、由6y=4,得y=4-6 | ||||
C、由
| ||||
| D、由4-x=2x,得2x-x=4 |
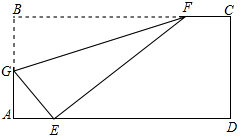 如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.
如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上,且AB=6,BC=10.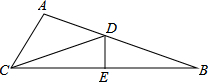 已知在△ABC中,∠ACB=60°,AC=2,BC=6,将△ABC沿着DE翻折,使点B与点C重合,折痕DE交AB于点D,交BC于点E,那么△ACD的面积为
已知在△ABC中,∠ACB=60°,AC=2,BC=6,将△ABC沿着DE翻折,使点B与点C重合,折痕DE交AB于点D,交BC于点E,那么△ACD的面积为 已知点A、B在反比例函数y=
已知点A、B在反比例函数y= 一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.
一辆园林喷灌车和一辆公交车分别从一条笔直公路两端点A、B同时出发匀速行驶,喷灌车中途停车在供水站加满水后继续以原速进行作业到达终点B,公交车到达A处进站检修,之后沿原路原点返回到点B.如图是两车与点A的距离y(千米)与运行时间t(时)的函数图象.