题目内容
3.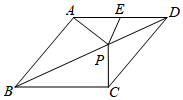 如图,点P为菱形ABCD对角线BD上一点,连接PA、PC.点E在边AD上,且∠AEP=∠DCP.
如图,点P为菱形ABCD对角线BD上一点,连接PA、PC.点E在边AD上,且∠AEP=∠DCP.求证:PC=PE.
分析 根据菱形的性质得到AD=CD,∠ADP=∠CDP,根据全等三角形的性质得到AP=CP,∠DCP=∠DAP,等量代换得到∠DAP=∠AEP,于是得到结论.
解答 证明:∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP,
在△ADP与△CDP中,$\left\{\begin{array}{l}{AD=CD}\\{∠ADP=∠CDP}\\{PD=PD}\end{array}\right.$,
∴△ADP≌△CDP,
∴AP=CP,∠DCP=∠DAP,
∵∠AEP=∠DCP,
∴∠DAP=∠AEP,
∴AP=PE,
∴PC=PE.
点评 本题考查了菱形的性质,全等三角形的判断和性质,等腰三角形的判定,熟练正确菱形的性质是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.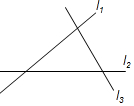 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
 如图,在平面直角坐标系中,已知点B(4,2),A(4,0).
如图,在平面直角坐标系中,已知点B(4,2),A(4,0).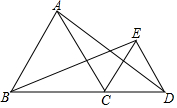 如图,点C在BD边上,且△ABC和△ECD都是等边三角形,图中有一对全等三角形可以看成是旋转变换得到的.一对全等三角形是△BCE≌△ACD,其旋转中心是点C,旋转角的度数是60°.
如图,点C在BD边上,且△ABC和△ECD都是等边三角形,图中有一对全等三角形可以看成是旋转变换得到的.一对全等三角形是△BCE≌△ACD,其旋转中心是点C,旋转角的度数是60°. 如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的.
如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转7次,每次旋转45度形成的.


