题目内容
7. 如图,AB=AC,D、E在BC上且AD=AE,AF⊥BC于点F则图中全等三角形有( )
如图,AB=AC,D、E在BC上且AD=AE,AF⊥BC于点F则图中全等三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
分析 由HL可判定△ABF≌△ACF和△ADF≌△AEF,进一步可判定△ABD≌△ACE和△ABE≌△ACD,可得出答案.
解答 解:
∵AF⊥BC,
∴∠AFB=∠AFC=90°,
在Rt△ABF和Rt△ACF中
$\left\{\begin{array}{l}{AB=AC}\\{AF=AF}\end{array}\right.$
∴Rt△ABF≌Rt△ACF(HL),
同理可得Rt△ADF≌Rt△AEF,
∴BF=CF,DF=EF,
∴BD=CE,BE=CD,
在△ABD和△ACE中
$\left\{\begin{array}{l}{AB=AC}\\{AD=AE}\\{BD=CE}\end{array}\right.$
∴△ABD≌△ACE(SSS),
同理可得△ABE≌△ACD,
综上可知全等的三角形共有4对,
故选D.
点评 本题主要考查三角形全等的判定方法,掌握全等三角形的五种判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
17. 如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )
 如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )
如图,?ABCD的对角线AC与BD相交于点O,E为CD边中点,BC=6cm,则OE的长为( )| A. | 2cm | B. | 3cm | C. | $\sqrt{6}$cm | D. | 2$\sqrt{3}$cm |
18. 如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )
如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )
 如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )
如图,平行四边形ABCD中,EF∥BC,AE:EB=2:3,EF=4,则AD的长为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 10 | D. | 16 |
15. 如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
 如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )| A. | 25 | B. | 20 | C. | 15 | D. | 10 |
2. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )| A. | x<3 | B. | $x>\frac{3}{2}$ | C. | x<$\frac{3}{2}$ | D. | x>3 |
12.不等式组$\left\{\begin{array}{l}x-1>0\\ x-3<0\end{array}\right.$的解集是( )
| A. | x>1 | B. | x<3 | C. | 1<x<3 | D. | 无解 |
19.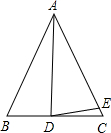 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
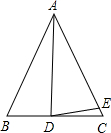 如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
16.某同学五天内每天完成家庭作业的时间(时)分别为2,3,2,1,2,则对这组数据的下列说法中错误的是
( )
( )
| A. | 平均数是2 | B. | 众数是2 | C. | 中位数是2 | D. | 方差是2 |
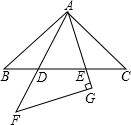 将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?
将两块完全相同的等腰直角三角形摆放成如图的样子,假设图形中的所有点、线都在同一平面内,图中有相似(不包括全等)三角形吗?如果有,请写出其中的一对,并给予说明其为什么相似?