题目内容
11.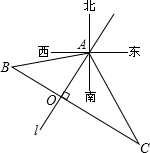 一辆货车在公路BC上由B向C行驶,一辆小汽车在公路l上由A沿AO方向行驶.已知两条公路互相垂直,A到BC的距离为100米,两条公路的交点O位于A的南偏西32°方向上,点B位于A的南偏西77°方向上,点C位于A的南偏东28°方向上.设两车同时开出且小汽车的速度是货车速度的2倍,求两车在行驶过程中的最近距离.
一辆货车在公路BC上由B向C行驶,一辆小汽车在公路l上由A沿AO方向行驶.已知两条公路互相垂直,A到BC的距离为100米,两条公路的交点O位于A的南偏西32°方向上,点B位于A的南偏西77°方向上,点C位于A的南偏东28°方向上.设两车同时开出且小汽车的速度是货车速度的2倍,求两车在行驶过程中的最近距离.
分析 首先计算出∠BAO和∠CAO的度数,进而可得OB=OA=100米,再根据勾股定理可得S2=(100-x)2+(100-2x)2,整理后求出S2最小值,进而可得两车在行驶过程中的最近距离.
解答 解:由题意得:∠BAO=77°-32°=45°,∠CAO=32°+28°=60°,
在Rt△AOB中,OB=OA=100米,
∵两车同时开出且小汽车的速度是货车速度的2倍,
∴当货车由B开出x米时,小汽车由A开出了2x米,设两车之间的距离为S,
则S2=(100-x)2+(100-2x)2=5x2-600x+20000=5(x-60)2+2000,
∴当x=60时,S2取得最小值2000,此时S的值为20$\sqrt{5}$米.
点评 此题主要考查了勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
19.代数式2x+7与-3互为相反数,则x值为( )
| A. | 2 | B. | -2 | C. | 5 | D. | -5 |
3.在实数0,-$\sqrt{3}$,1,-2中最小的是( )
| A. | -2 | B. | -$\sqrt{3}$ | C. | 0 | D. | 1 |
20.若二次函数y=ax2+bx+c的图象与x轴有两个交点,坐标为A(m,0),B(n,0),且m<n,图象上有一点C(3,P)在x轴下方,则下列判断正确的是( )
| A. | b2-4ac≥0 | B. | m<3<n | C. | (m-3)(n-3)<0 | D. | 以上都不对 |