题目内容
16. 如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.
如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.
分析 作BD⊥AC,根据∠C=45°,BC=2$\sqrt{2}$,AC=6,可得BD,CD的长,从而可以求得AD的长,从而可以解答本题.
解答 解:作BD⊥AC于点D,如下图所示:
∵∠C=45°,BC=2$\sqrt{2}$,BD⊥AC,
∴∠BDC=90°,BD=CD,BD2+CD2=BC2.
∴BD=CD=2.
∵AC=6,CD=2,
∴AD=4.
∴tanA=$\frac{BD}{AD}=\frac{2}{4}=\frac{1}{2}$,${S}_{△ABC}=\frac{AC×BD}{2}=\frac{6×2}{2}=6$.
即tanA=$\frac{1}{2}$,△ABC的面积是6.
点评 本题考查解直角三角形、三角形的面积,解题的关键是作合适的辅助线,明确三角函数指的是哪两条边的比值.

练习册系列答案
相关题目
8.下列一次函数中,y随x增大而减小的是( )
| A. | y=2x | B. | y=3x-2 | C. | y=-5x+2 | D. | y=2x-2 |
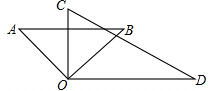 如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由.
如图所示,小红将两个直角三角形AOB,COD摆放在桌面上,使得它们的直角顶点重合在一起,小红得到出两个结论:(1)∠AOC=∠BOD;(2)∠AOD与∠BOC互补,请你判断她得出的两个结论是否正确,并说明理由. 如图所示,已知点C在线段AB上,且BC=4AC,点D是线段AB的中点,若CD=9cm,试求BC的长.
如图所示,已知点C在线段AB上,且BC=4AC,点D是线段AB的中点,若CD=9cm,试求BC的长.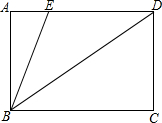 已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为24.
已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为24.