题目内容
5.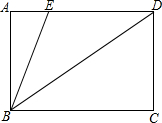 已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为24.
已知矩形ABCD,点E在AD边上,连接BE、BD,∠BED=2∠BDC,BE=25,BC=32,则CD的长度为24.
分析 过E作EF⊥BD于F,根据矩形的性质得到∠C=∠ADC=90°,于是得到∠ADB+∠BDC=90°,根据已知条件推出180°-∠AEB=2(90°-∠ADB),得到∠AEB=2∠EDB,根据等腰三角形的性质得到BF=$\frac{1}{2}$BD,由平行线的性质得到∠ADB=∠DBC,等量代换得到∠EBF=∠DBC,推出△EBF∽△DBC,根据相似三角形的性质得到$\frac{BE}{BD}=\frac{BF}{BC}$,求得BD=40,由勾股定理即可得到结论.
解答 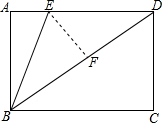 解:过E作EF⊥BD于F,
解:过E作EF⊥BD于F,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90°,
∴∠ADB+∠BDC=90°,
∵∠BED=2∠BDC,
∴180°-∠AEB=2(90°-∠ADB),
∴∠AEB=2∠EDB,
∵∠AEB=∠ADB+∠EBD,
∴∠EDB=∠EBD,
∴BE=DE,
∴BF=$\frac{1}{2}$BD,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠EBF=∠DBC,
∴△EBF∽△DBC,
∴$\frac{BE}{BD}=\frac{BF}{BC}$,
∴BD2=2BC•BE=2×25×32=402,
∴BD=40,
∴CD=$\sqrt{B{D}^{2}-B{C}^{2}}$=24.
故答案为:24.
点评 本题考查了矩形的性质,相似三角形的判定和性质,平行线的性质,外角的性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.
如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.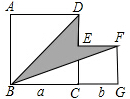 如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积.
如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积.