题目内容
19. 如图,⊙O半径为5,OM⊥弦AB于点M,若OM=3,则弦AB长为8.
如图,⊙O半径为5,OM⊥弦AB于点M,若OM=3,则弦AB长为8.
分析 连接OA,根据勾股定理求出AM的长,根据垂径定理得到AB=2AM,得到答案.
解答 解:连接OA,
∵OM⊥AB,
∴AB=2AM,
在Rt△AOM中,OA=5,OM=3,
由勾股定理得,AM=4,
∴AB=2AM=8,
故答案为:8.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分线是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
10.若方程6kx-2y=8有一组解$\left\{\begin{array}{l}x=-3\\ y=2\end{array}$,则k的值等于( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
4. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
9.已知两个数的和为正数,则( )
| A. | 一个加数为正,另一个加数为零 | |
| B. | 两个加数都为正数 | |
| C. | 两个加数一正一负,且正数的绝对值大于负数的绝对值 | |
| D. | 以上三种都有可能 |
 如图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=3cm,则AC=9 cm.
如图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=3cm,则AC=9 cm. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,若正方形的边长是2,则图中阴影部分的面积等于1.
如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,若正方形的边长是2,则图中阴影部分的面积等于1.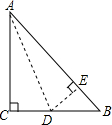 有一块直角三角形纸片,两直角边AC=12cm,BC=5cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为2.4cm.
有一块直角三角形纸片,两直角边AC=12cm,BC=5cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为2.4cm. 如图:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.
如图:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.