题目内容
13.直线y=kx(k≠0)交抛物线y=x2-2x-2于点A,B,若OA=OB,求k的值.分析 联立两函数解析式消掉y,整理得到关于x的一元二次方程,再根据OA=OB,点A、B的横坐标互为相反数列方程求解即可.
解答 解:联立$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-2x-2}\end{array}\right.$,
消掉y得,x2-2x-2=kx,
整理得,x2-(k+2)x-2=0,
∵OA=OB,
∴x1=x2,
∴k+2=0,
解得k=-2.
点评 本题考查了二次函数的性质,正比例函数的性质,熟记各性质并判断出点A、B的横坐标相等是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
8.有50个同学排成一队,第一次从前往后报数(按1,2,3,…的顺序),报到奇数的同学退出队伍,第二次从后往前报数(按1,2,3,…的顺序),报到奇数的同学退出队伍,第三次又从前往后报数,第四次又从后往前报数,如此继续下去…则最后留下来的同学第一次报的数是( )
| A. | 16 | B. | 24 | C. | 32 | D. | 48 |
2.已知a+b=2,ab=1,化简(a-2)(b-2)的结果为( )
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
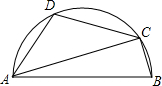 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,则∠D=110°.