题目内容
(1)如图1,在△ABC中,AB=AC,∠A=9°,BD平分∠ABC,DE⊥BC,垂足为E,试说明BC=AB+AD.
(2)如图2,在△ABC中,BD平分∠ABC,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12.求DE的长.

(2)如图2,在△ABC中,BD平分∠ABC,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12.求DE的长.

考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)求出∠ABD=∠EBD,∠A=∠BED=90°,根据AAS推出△ABD≌△EBD,根据全等三角形的性质得出AD=DE,AB=BE,求出ED=EC,AD=EC,即可得出答案;
(2)作DF⊥BC于F,根据S△ABC=S△ABD+S△BCD和DE=x得出方程
•16x+
•12x=70,求出方程的解即可.
(2)作DF⊥BC于F,根据S△ABC=S△ABD+S△BCD和DE=x得出方程
| 1 |
| 2 |
| 1 |
| 2 |
解答: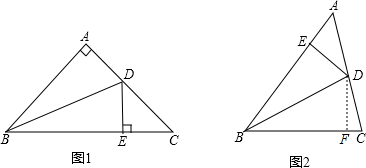
(1)解:∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵∠A=90°,DE⊥BC,
∴∠A=∠BED=90°,
在△ABD和△EBD中
∴△ABD≌△EBD,
∴AD=DE,AB=BE,
∵AB=AC,∠A=90°,
∴∠C=45°,
∵∠BED=90°,
∴∠EDC=∠C=45°,
∴ED=EC,
∴AD=EC,
∵BC=BE+EC,
∴BC=AB+AD;
(2)作DF⊥BC于F,
∵由(1)得:ED=DF,
∴S△ABC=S△ABD+S△BCD
设DE=x,
•16x+
•12x=70,
∴x=5,
即DE=5.

(1)解:∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵∠A=90°,DE⊥BC,
∴∠A=∠BED=90°,
在△ABD和△EBD中
|
∴△ABD≌△EBD,
∴AD=DE,AB=BE,
∵AB=AC,∠A=90°,
∴∠C=45°,
∵∠BED=90°,
∴∠EDC=∠C=45°,
∴ED=EC,
∴AD=EC,
∵BC=BE+EC,
∴BC=AB+AD;
(2)作DF⊥BC于F,
∵由(1)得:ED=DF,
∴S△ABC=S△ABD+S△BCD
设DE=x,
| 1 |
| 2 |
| 1 |
| 2 |
∴x=5,
即DE=5.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定的应用,能运用性质定理进行推理是解此题的关键,综合性比较强.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图,在如图网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正切值是( )
如图,在如图网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正切值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法中,正确的个数是( )
(1)相等的角是对顶角;(2)平面内,过一点有且只有一条直线和已知直线垂直;
(3)两条直线相交有且只有一个交点;(4)两条直线相交成直角,则这个两条直线互相垂直.
(1)相等的角是对顶角;(2)平面内,过一点有且只有一条直线和已知直线垂直;
(3)两条直线相交有且只有一个交点;(4)两条直线相交成直角,则这个两条直线互相垂直.
| A、1 | B、2 | C、3 | D、4 |
 数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )
数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )| A、0.38 | B、0.4 |
| C、0.16 | D、0.08 |
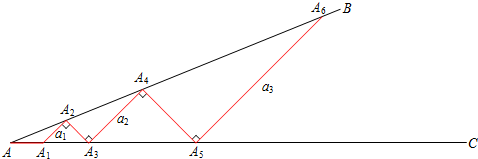
 如图,已知:S△ABC=1,AE=ED,BD=
如图,已知:S△ABC=1,AE=ED,BD= 观察猜想:我国著名的数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”说明数形结合是一种重要的数学方法,许多重要的计算转化成图形后,非常巧妙而简单,观察图形:
观察猜想:我国著名的数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”说明数形结合是一种重要的数学方法,许多重要的计算转化成图形后,非常巧妙而简单,观察图形: