题目内容
直线y=-
x+6与x轴,y轴分别交于P,Q两点,把△POQ沿PQ对折,点O落在R处,则点R的坐标为 .
| 3 |
考点:翻折变换(折叠问题),一次函数图象上点的坐标特征
专题:
分析:连结OR,设OR交PQ于A,根据折叠的性质得到PQ垂直平分OR,根据两个一次函数的图象垂直的性质得到直线OR的解析式为y=
x,设R点坐标为(a,
a),则利用线段中点公式得到A点坐标为(
a,
a),然后把A点坐标代入y=-
x+6求出a,从而确定R点坐标.
| ||
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
| 3 |
解答: 解:∵把△POQ沿PQ对折,点O落在R处,连结OR,设OR交PQ于A,
解:∵把△POQ沿PQ对折,点O落在R处,连结OR,设OR交PQ于A,
∴PQ垂直平分OR,
∴直线OR的解析式为y=
x,
设R点坐标为(a,
a),则A点坐标为(
a,
a),
把A(
a,
a)代入y=-
x+6,
得-
×
a+6=
a,
解得a=3
,
∴R点坐标为(3
,3).
故答案为(3
,3).
 解:∵把△POQ沿PQ对折,点O落在R处,连结OR,设OR交PQ于A,
解:∵把△POQ沿PQ对折,点O落在R处,连结OR,设OR交PQ于A,∴PQ垂直平分OR,
∴直线OR的解析式为y=
| ||
| 3 |
设R点坐标为(a,
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
把A(
| 1 |
| 2 |
| ||
| 6 |
| 3 |
得-
| 3 |
| 1 |
| 2 |
| ||
| 6 |
解得a=3
| 3 |
∴R点坐标为(3
| 3 |
故答案为(3
| 3 |
点评:本题考查了翻折变换(折叠问题),一次函数图象上点的坐标特征,掌握互相垂直的两直线斜率之积为-1是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.
如图,在△ABC中,∠ACB=90°,AC=BC,点P在AB上,AD⊥CP于D,BE⊥CP于E,已知CD=3cm,求BE的长.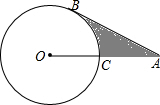 如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
如图,AB是圆O的切线,切点为B,AO交圆O与点C,且AC=OC.
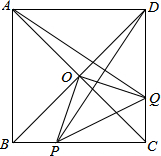 如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形.
如图,O是正方形ABCD对角线的交点,Q是DC上任意一点,过点D作DE⊥AQ交BC于点P,求证:△OPQ是等腰直角三角形. 如图,∠ADB=
如图,∠ADB=