题目内容
1.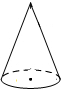 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
分析 根据圆锥的侧面展开图的弧长=2πr=$\frac{nπl}{180}$,求出r以及圆锥的高h即可解决问题.
解答 解:设圆锥的底面半径为r,高为h.
由题意:2πr=$\frac{120×π×6}{180}$,解得r=2,h=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$,
所以tanα=$\frac{2}{4\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,圆锥的主视图的面积=$\frac{1}{2}$×4×4$\sqrt{2}$=8$\sqrt{2}$,表面积=4π+$\frac{1}{2}$×4π×6=16π.
∴选项A、B、C错误,D正确.
故选D.
点评 本题考查圆锥的有关知识,记住侧面展开图的弧长=2πr=$\frac{nπl}{180}$,圆锥的表面积=πr2+πrl是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
6.某天蔬菜经营户用120元批发了西兰花和胡萝卜共60kg到菜市场零售,西兰花和胡萝卜当天的批发价和零售价如表所示:
如果他当天全部卖完这些西兰花和胡萝卜可获得利润多少元.
| 品名 | 西兰花 | 胡萝卜 |
| 批发价(元/kg) | 2.8 | 1.6 |
| 零售价(元/kg) | 3.8 | 2.5 |
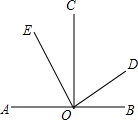 如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°.
如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°.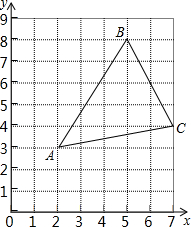 如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.
如图,在三角形ABC中,点A在网格中用有序数对(2,3)表示,点B用(5,8)表示.