题目内容
已知关于x的方程|x2-2
x+1|=k有四个不同的实根,求k的取值范围.
| 3 |
考点:抛物线与x轴的交点
专题:数形结合
分析:将方程问题转化为二次函数与一次函数图象的交点问题,画出函数图象,利用图象即可轻松解答.
解答: 解:∵关于x的方程|x2-2
解:∵关于x的方程|x2-2
x+1|=k有四个不同的实根,
即函数y=|x2-2
x+1|与函数y=k的图象有四个不同的交点,
如图作出y=|x2-2
x+1|的图象,
再作出y=k的图象,
从图象可以看出当0<k<2时,
直线y=k与y=|x2-2
x+1|的图象才有四个不同交点,
也即原方程有四个不同的实根.
 解:∵关于x的方程|x2-2
解:∵关于x的方程|x2-2| 3 |
即函数y=|x2-2
| 3 |
如图作出y=|x2-2
| 3 |
再作出y=k的图象,
从图象可以看出当0<k<2时,
直线y=k与y=|x2-2
| 3 |
也即原方程有四个不同的实根.
点评:此题考查了函数与方程的关系,作图时要注意绝对值的作用:无论x取何值,y值均为正数.

练习册系列答案
相关题目
(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)是完全平方式,则a,b,c的关系可以写成( )
| A、a<b<c |
| B、(a-b)2+(b-c)2=0 |
| C、c<a<b |
| D、a=b≠c |
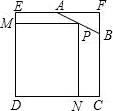 如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )