题目内容
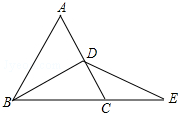 已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.
已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.(1)证明:△BDE是等腰三角形;
(2)若AB=2,求DE的长度.
考点:等边三角形的性质,等腰三角形的判定,勾股定理
专题:
分析:(1)由△ABC为等边三角形,可求出∠BDC=90°,由△DCE是等腰三角形求出∠CDE=∠CED=30°,根据等角对等边即可证得;
(2)由勾股定理求出BD即可求得.
(2)由勾股定理求出BD即可求得.
解答:(1)证明:∵△ABC为等边三角形,
∴∠DCB=60°
∵CE=CD∴∠CED=∠CDE,
∵∠DCB=∠CED+∠CDE=60°
∴∠CED=∠CDE=30°,
∵BD为中线∴∠DBC=30°,
∴∠DBC=∠CED∴BD=DE
∴△BDE是等腰三角形;
(2)解:∵BD为中线,
∴AD=
AC=1,BD⊥AC,
∴∠ADB=90°
在Rt△ABD中,由勾股定理得:
∴BD=
,
∴DE=BD=
.
∴∠DCB=60°
∵CE=CD∴∠CED=∠CDE,
∵∠DCB=∠CED+∠CDE=60°
∴∠CED=∠CDE=30°,
∵BD为中线∴∠DBC=30°,
∴∠DBC=∠CED∴BD=DE
∴△BDE是等腰三角形;
(2)解:∵BD为中线,
∴AD=
| 1 |
| 2 |
∴∠ADB=90°
在Rt△ABD中,由勾股定理得:
∴BD=
| 3 |
∴DE=BD=
| 3 |
点评:本题考查了等边三角形性质,勾股定理,等腰三角形性质,三角形的外角性质等知识点的应用,关键是求出DE=BD和求出BD的长.

练习册系列答案
相关题目
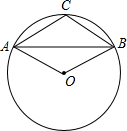 如图,已知A、B、C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是( )
如图,已知A、B、C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是( )| A、2 | ||
B、
| ||
C、
| ||
D、2
|
 一次函数y=kx+b图象经过点(0,3)和(4,6).
一次函数y=kx+b图象经过点(0,3)和(4,6).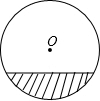 如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为
如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为
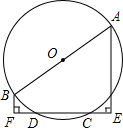 已知如图,AB为⊙O直径,CD为⊙O的弦,AE⊥CD交DC延长线于E,BF⊥CD,交CD延长线于F.
已知如图,AB为⊙O直径,CD为⊙O的弦,AE⊥CD交DC延长线于E,BF⊥CD,交CD延长线于F. 作图题:(要求保留作图痕迹,不写作法)
作图题:(要求保留作图痕迹,不写作法)