题目内容
 如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为
如图是一条水平铺设的直径为2米的通水管道横截面,当管道中水深为0.4米时,水面宽为考点:垂径定理的应用,勾股定理
专题:
分析:过O作OE⊥AB交AB于点D,连接OA、OB,由垂径定理可知AD=
AB,再OA=1米,则OD=0.6米,再在Rt△OAD中利用勾股定理即可求出AD的值,进而求出AB=2AD
| 1 |
| 2 |
解答: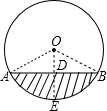 解:过O作OE⊥AB交AB于点D,连接OA、OB,则AD=
解:过O作OE⊥AB交AB于点D,连接OA、OB,则AD=
AB.
∵⊙O的直径为2米,
∴OE=1米.
又∵DE=0.4米,
∴OD=OE-DE=0.6米,
在Rt△OAD中,OA2=AD2+OD2,即12=AD2+0.62,
解得AD=0.8米,
故此输水管道的直径=2AD=1.6米.
故答案是:1.6米.
 解:过O作OE⊥AB交AB于点D,连接OA、OB,则AD=
解:过O作OE⊥AB交AB于点D,连接OA、OB,则AD=| 1 |
| 2 |
∵⊙O的直径为2米,
∴OE=1米.
又∵DE=0.4米,
∴OD=OE-DE=0.6米,
在Rt△OAD中,OA2=AD2+OD2,即12=AD2+0.62,
解得AD=0.8米,
故此输水管道的直径=2AD=1.6米.
故答案是:1.6米.
点评:本题考查的是垂径定理的应用,根据题意画出图形,作出辅助线,构造出直角三角形,再利用勾股定理求解是解答此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

 如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大?
如图所示是某酒店门前的台阶,现该酒店经理要在台阶上铺上一块红地毯,问这块红地毯至少要多大? 2008年奥运会吉祥物五个福娃(贝贝、晶晶、欢欢、迎迎、妮妮)的卡通画和奥运五环标志,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后能围成如图所示正方体的图形是( )
2008年奥运会吉祥物五个福娃(贝贝、晶晶、欢欢、迎迎、妮妮)的卡通画和奥运五环标志,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后能围成如图所示正方体的图形是( )



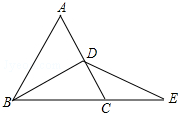 已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.
已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.