题目内容
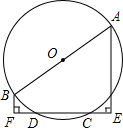 已知如图,AB为⊙O直径,CD为⊙O的弦,AE⊥CD交DC延长线于E,BF⊥CD,交CD延长线于F.
已知如图,AB为⊙O直径,CD为⊙O的弦,AE⊥CD交DC延长线于E,BF⊥CD,交CD延长线于F.(1)求证:CE=DF;
(2)若AB=10cm,CD=6cm,求AE+BF的值.
考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:(1)如图,过点O作OG⊥CD,运用垂径定理及平行线等分线段定理即可解决问题.
(2)如图,连接OD,运用勾股定理求出OG的长度,根据梯形的中位线定理即可解决问题.
(2)如图,连接OD,运用勾股定理求出OG的长度,根据梯形的中位线定理即可解决问题.
解答: (1)证明:如图,过点O作OG⊥CD于点G;
(1)证明:如图,过点O作OG⊥CD于点G;
则DG=CD;
∵BF⊥EF,AE⊥EF,
∴BF∥OG∥AE,而OA=OB,
∴GF=GE,
∴GF-GD=GE-CE,
即CE=DF.
(2)解:如图,连接OD;
∵AB=10,CD=6,
∴OD=5,DG=3;
由勾股定理得:OG2=OD2-DG2=25-9=16,
∴OG=4;
由(1)知:OG为梯形ABFE的中位线,
∴AE+BF=2OG=8,
即AE+BF的值为8.
 (1)证明:如图,过点O作OG⊥CD于点G;
(1)证明:如图,过点O作OG⊥CD于点G;则DG=CD;
∵BF⊥EF,AE⊥EF,
∴BF∥OG∥AE,而OA=OB,
∴GF=GE,
∴GF-GD=GE-CE,
即CE=DF.
(2)解:如图,连接OD;
∵AB=10,CD=6,
∴OD=5,DG=3;
由勾股定理得:OG2=OD2-DG2=25-9=16,
∴OG=4;
由(1)知:OG为梯形ABFE的中位线,
∴AE+BF=2OG=8,
即AE+BF的值为8.
点评:该命题以圆为载体,在重点考查垂径定理、梯形的中位线定理等几何知识点的同时,还渗透了对勾股定理等知识点的考查;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 2008年奥运会吉祥物五个福娃(贝贝、晶晶、欢欢、迎迎、妮妮)的卡通画和奥运五环标志,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后能围成如图所示正方体的图形是( )
2008年奥运会吉祥物五个福娃(贝贝、晶晶、欢欢、迎迎、妮妮)的卡通画和奥运五环标志,如果分别用“贝、晶、欢、迎、妮”五个字来表示五个福娃,那么折叠后能围成如图所示正方体的图形是( )A、 |
B、 |
C、 |
D、 |
下列函数中,是二次函数的为( )
| A、y=8x2+1 | ||
| B、y=8x+1 | ||
C、y=
| ||
D、y=
|
如果方程xm2-7-x+3=0是关于x的一元二次方程,那么m的值为( )
| A、±3 | B、3 |
| C、-3 | D、以上都不对 |

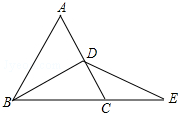 已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.
已知:如图,△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE.