题目内容
6.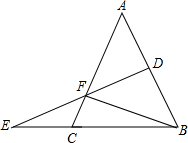 如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )
如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )| A. | 16,40° | B. | 8,50° | C. | 16,50° | D. | 8,40° |
分析 根据线段垂直平分线的定义和互余的性质求出∠AFD,根据对顶角相等求出∠EFC;根据线段垂直平分线的性质得到FA=FB,根据三角形周长公式计算即可.
解答 解:∵FD⊥AB,∠A=50°,
∴∠AFD=40°,
∴∠EFC=∠AFD=40°,
∵DF是AB的垂直平分线,
∴FA=FB,
∴△BCF的周长=BC+CF+FB=BC+CF+FA=BC+AC=16.
故选:A.
点评 本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
16.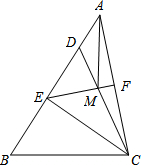 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.若∠BAC=45°,AM=4,DM=3,则BC的长度为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
14. 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )| A. | $\frac{23}{9}$ | B. | $\frac{128}{9}$ | C. | 16 | D. | $\frac{15}{4}$ |
1.在下列长度的四组线段中,不能组成直角三角形的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 1,1,$\sqrt{2}$ | D. | 4,5,6 |
11.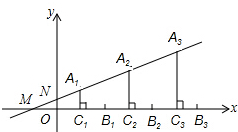 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
15.方程2x2-ax+7=0,有一根是$\frac{1}{2}$,则另一根为( )
| A. | 7 | B. | 7.5 | C. | -7 | D. | 15 |
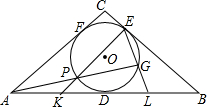 在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL.
在等腰△ABC中,AC=BC,其内切圆分别与边AB、BC、CA切于点D、E、F.一条过点A且异于AE的直线交△ABC的内切圆于点P、G,EP、EG分别交AB于点K、L.求证:DK=DL. 如图,用三个大写字母表示∠1为∠MCB;∠2为∠AMC;∠3为∠CAN.
如图,用三个大写字母表示∠1为∠MCB;∠2为∠AMC;∠3为∠CAN.