题目内容
先化简,再求值: 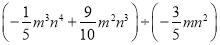 ,其中
,其中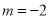 ,
, 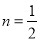 .
.
 【解析】试题分析:根据多项式除以单项式的法则进行化简,再把字母的值代入运算即可.
试题解析:原式,
当, 时,
原式.
【解析】试题分析:根据多项式除以单项式的法则进行化简,再把字母的值代入运算即可.
试题解析:原式,
当, 时,
原式.
练习册系列答案
相关题目
若(2x+1)0=1,则x的取值范围是_____.
 x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0,解得,所以当(2x+1)0=1,x的取值范围是.
x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0,解得,所以当(2x+1)0=1,x的取值范围是. 多项式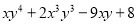 的次数是( )
的次数是( )
A. 3 B. 4 C. 5 D. 6
 D
【解析】多项式中最高单项式的次数叫做多项式的次数,由此可得多项式的次数是6次,故选D.
D
【解析】多项式中最高单项式的次数叫做多项式的次数,由此可得多项式的次数是6次,故选D. 草地上放置AB两个小球,它们之间的距离是10cm,若小球C可以在草地上任意摆放,那么小球C到A,B两球的距离之和的最小值为( )
A. 10cm B. 9cm C. 6cm D. 不能确定
 A
【解析】试题分析:当小球C在线段AB上时,根据两点之间,线段最短可知此时小球C到A、B两球距离之和最小,最小值为线段AB的长,即10cm.
故选A.
A
【解析】试题分析:当小球C在线段AB上时,根据两点之间,线段最短可知此时小球C到A、B两球距离之和最小,最小值为线段AB的长,即10cm.
故选A. 下面用代数式表示正确的是( )
A. -a的平方表示为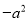 B. a与比a大2的数的积表示为
B. a与比a大2的数的积表示为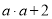
C. a与b的和的平方表示为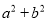 D. a,b两数差的平方表示为
D. a,b两数差的平方表示为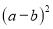
 D
【解析】试题分析:A、-a的平方表示为(-a)2,故此选项错误;
B、a与比a大2的数的积表示为a(a+2),故此选项错误;
C、a与b的和的平方表示为(a+b)2,故此选项错误;
D、a,b两数差的平方表示为(a-b)2,故此选项错误.
故选D.
D
【解析】试题分析:A、-a的平方表示为(-a)2,故此选项错误;
B、a与比a大2的数的积表示为a(a+2),故此选项错误;
C、a与b的和的平方表示为(a+b)2,故此选项错误;
D、a,b两数差的平方表示为(a-b)2,故此选项错误.
故选D. 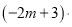 __________
__________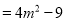 ,
, 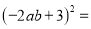 __________.
__________.
 【解析】试题解析:(1) 故填(?2m?3);
故填
故答案为:(?2m?3),
【解析】试题解析:(1) 故填(?2m?3);
故填
故答案为:(?2m?3), 如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:
①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn,你认为其中正确的有( )
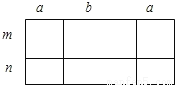
A. ①② B. ③④ C. ①②③ D. ①②③④
 D
【解析】①大长方形的长为2a+b,宽为m+n,利用长方形的面积公式,表示即可;
②长方形的面积等于左边,中间及右边的长方形面积之和,表示即可;
③长方形的面积等于上下两个长方形面积之和,表示即可;
④长方形的面积由6个长方形的面积之和,表示即可.
解答:【解析】
①(2a+b)(m+n),本选项正确;
②2a(m+n)+b(m+n),本选项正确;
③m(2a+b)+n(...
D
【解析】①大长方形的长为2a+b,宽为m+n,利用长方形的面积公式,表示即可;
②长方形的面积等于左边,中间及右边的长方形面积之和,表示即可;
③长方形的面积等于上下两个长方形面积之和,表示即可;
④长方形的面积由6个长方形的面积之和,表示即可.
解答:【解析】
①(2a+b)(m+n),本选项正确;
②2a(m+n)+b(m+n),本选项正确;
③m(2a+b)+n(... 小伟向一袋中装进a只红球,b只白球,它们除颜色外,无其他差别.小红从袋中任意摸出一球,问他摸出的球是红球的概率为( )
A. 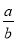 B.
B. 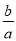 C.
C. 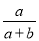 D.
D. 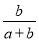
 C
【解析】袋中装进a只红球,b只白球,共有球(a+b)只,所以从袋中任意摸出一球,摸出的球是红球的概率等于,故选C.
C
【解析】袋中装进a只红球,b只白球,共有球(a+b)只,所以从袋中任意摸出一球,摸出的球是红球的概率等于,故选C. 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=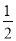 ∠BMN
∠BMN
同理∠GNM=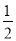 ∠DNM.
∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
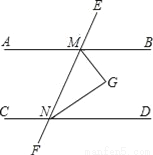
 已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(...
已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG.
【解析】试题分析:(1)根据平行线的性质进行填空即可;
(2)根据的特点作出结论.
试题解析:(1)∵MG平分∠BMN(已知)
(角平分线的定义),
同理
∵ABCD(已知),
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知; MG⊥NG;
(... 
