题目内容
8.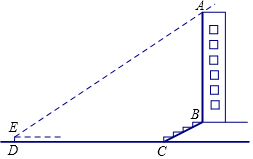 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,$\sqrt{3}$≈1.73.)
分析 延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
解答  解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,$\frac{BF}{CF}$=i=1:$\sqrt{3}$,
∴设BF=k,则CF=$\sqrt{3}$,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=6$\sqrt{3}$.
∵DF=DC+CF,
∴DF=40+6$\sqrt{3}$.
∵在Rt△AEH中,tan∠AEH=$\frac{AH}{EH}$,
∴AH=tan38°×(40+6$\sqrt{3}$)≈39.30(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=39.30-4.5=34.80.
答:大楼AB的高度约为34.80米.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.

练习册系列答案
相关题目
 如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形,图中以A、B为顶点,面积为4的阵点平行四边形的个数有( )
如图,由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形,图中以A、B为顶点,面积为4的阵点平行四边形的个数有( )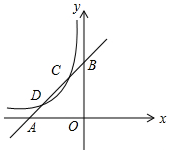 如图,已知直线y1=x+m与x轴,y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$分别交于点C、D,且点C的坐标为(-1,2),则不等式$\frac{k}{x}$>x+m的解集为x<2或-1<x<0;.
如图,已知直线y1=x+m与x轴,y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$分别交于点C、D,且点C的坐标为(-1,2),则不等式$\frac{k}{x}$>x+m的解集为x<2或-1<x<0;.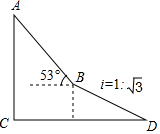 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°=$\frac{4}{5}$,cos$\frac{3}{5}$=$\frac{3}{5}$,tan53°=$\frac{4}{3}$,$\sqrt{3}$≈1.732,结果精确到0.1米)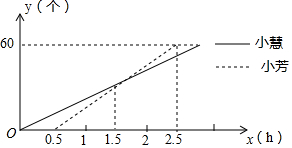 某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题:
某厂要加工一批新型零件,让小慧和小芳每人试加工60个,小慧一上班就开始试加工,小芳接受半小时培训后再开始试加工,如图所示为小慧和小芳试加工过程中加工的零件数y(个)与加工时间x(h)之间的函数图象,请根据图象所提供的信息解答下列问题: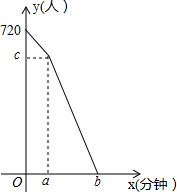 五一假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有720人排队检票,检票开始后,仍有旅客继续前来排队检票进站,设旅客按固定的速度增加,检票口检票的速度也是固定的,检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人,已知检票的前a分钟只开放了2个检票口,a分钟后又开放了2个检票窗口,候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.(b>a)
五一假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有720人排队检票,检票开始后,仍有旅客继续前来排队检票进站,设旅客按固定的速度增加,检票口检票的速度也是固定的,检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人,已知检票的前a分钟只开放了2个检票口,a分钟后又开放了2个检票窗口,候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.(b>a)