题目内容
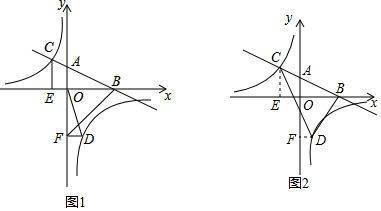
3.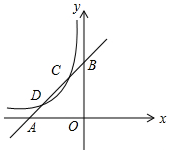 如图,已知直线y1=x+m与x轴,y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$分别交于点C、D,且点C的坐标为(-1,2),则不等式$\frac{k}{x}$>x+m的解集为x<2或-1<x<0;.
如图,已知直线y1=x+m与x轴,y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$分别交于点C、D,且点C的坐标为(-1,2),则不等式$\frac{k}{x}$>x+m的解集为x<2或-1<x<0;.
分析 先根据C的坐标求直线AB的解析式,代入可求反比例的解析式,根据图象可得结论.
解答 解:把点C的坐标为(-1,2)代入y1=x+m中得:2=-1+m,m=3,
∴直线AB的解析式为:y1=x+3,
∵点C(-1,2)在双曲线y2=$\frac{k}{x}$上,
∴k=-1×2=-2,
∴双曲线的解析式为:y2=-$\frac{2}{x}$,
则$\left\{\begin{array}{l}{y=x+3}\\{y=-\frac{2}{x}}\end{array}\right.$,
x+3=-$\frac{2}{x}$,
x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1,x2=-2,
∴D(-2,1),
则不等式$\frac{k}{x}$>x+m的解集为:x<2或-1<x<0;
故答案为:x<2或-1<x<0.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法求出一次函数和反比例函数的解析式,主要考查学生运用性质进行计算的能力,题目比较好,有一定的难度,用了数形结合的思想.

练习册系列答案
相关题目
18.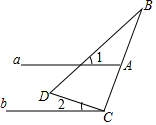 如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )
 如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )| A. | 20° | B. | 40° | C. | 30° | D. | 25° |
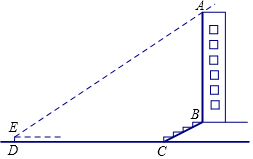 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$,在离C点40米的D处,用测角仪测得大楼顶端A的仰角为38°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)