题目内容
若(x2+y2)2-6(x2+y2)-7=0,则x2+y2= .
考点:解一元二次方程-因式分解法
专题:
分析:令x2+y2=a,将原方程化为a2-6a-7=0,求出a的值即可由于a是非负数,故负值舍去.
解答:解:令x2+y2=a,
则原方程可化为a2-6a-7=0,
因式分解,得(a+1)(a-7)=0,
解得a=-1(负值舍去),或a=7,
故答案为7.
则原方程可化为a2-6a-7=0,
因式分解,得(a+1)(a-7)=0,
解得a=-1(负值舍去),或a=7,
故答案为7.
点评:本题考查了解一元二次方程--因式分解法,熟悉换元法和十字相乘法是解题的关键.

练习册系列答案
相关题目
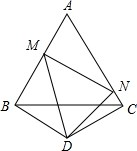 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由. 如图,抛物线y=ax2+bx+c,则a
如图,抛物线y=ax2+bx+c,则a 如图,抛物线y=ax2+bx+c与x轴的交点分别为(-1,0),(3,0),则
如图,抛物线y=ax2+bx+c与x轴的交点分别为(-1,0),(3,0),则