题目内容
已知△ABC中，a、b、c分别为△ABC三边，满足a2+b2+c2-ab-bc-ca=0，判断三角形的形状．
考点：因式分解的应用
专题：
分析：对a2+b2+c2-ab-bc-ca=0进行因式分解可得（a-b）2+（b-c）2+（c-a）2=0，再由非负数的性质可求得a=b=c，所以三角形为等边三角形．
解答：解：△ABC为等边三角形．
理由：∵a2+b2+c2-ab-bc-ac=0，
∴2a2+2b2+2c2-2ab-2bc-2ac=0，
a2+b2-2ab+b2+c2-2bc+a2+c2-2ac=0，
即（a-b）2+（b-c）2+（c-a）2=0，
∴a-b=0，b-c=0，c-a=0，
∴a=b=c，△ABC为等边三角形．
理由：∵a2+b2+c2-ab-bc-ac=0，
∴2a2+2b2+2c2-2ab-2bc-2ac=0，
a2+b2-2ab+b2+c2-2bc+a2+c2-2ac=0，
即（a-b）2+（b-c）2+（c-a）2=0，
∴a-b=0，b-c=0，c-a=0，
∴a=b=c，△ABC为等边三角形．
点评：本题主要考查因式分解的应用，解题的关键是把所给式子进行因式分解，再利用非负数的性质得出a、b、c之间的关系．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
相关题目
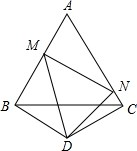如图，△ABC是边长为a的等边三角形，△BCD中，BD=CD，∠BDC=120°，点M，N分别在AB，AC上，且∠MDN=60°．试问：△AMN的周长和面积是否随着点M，N的位置的改变而改变，请说明理由．
已知，如图，在△ABC中，∠ABC的平分线与∠ACB的外角平分线交于点D．