题目内容
已知关于x的一元二次方程x2-(2k-1)x+k2-k-2=0.
(1)求证:方程有两个不相等的实数根;
(2)△ABC中,一边的长为5,其余两边的长是该方程的两个实数根,当△ABC是等腰三角形时,求k的值及△ABC的周长.
(1)求证:方程有两个不相等的实数根;
(2)△ABC中,一边的长为5,其余两边的长是该方程的两个实数根,当△ABC是等腰三角形时,求k的值及△ABC的周长.
考点:根的判别式,一元二次方程的解,三角形三边关系,等腰三角形的性质
专题:
分析:(1)先求出△的值,再根据△的意义即可得到结论;
(2)根据方程有两个不相等的实数根,△ABC其余两边的长是该方程的两个实数根,得出△ABC的腰长为5,再把5的值代入求出k的值,最后根据周长公式即可求出答案.
(2)根据方程有两个不相等的实数根,△ABC其余两边的长是该方程的两个实数根,得出△ABC的腰长为5,再把5的值代入求出k的值,最后根据周长公式即可求出答案.
解答:解:(1)∵△=[-(2k-1)]2-4×1×(k2-k-2)=9>0,
∴方程有两个不相等的实数根;
(2)∵方程有两个不相等的实数根,△ABC其余两边的长是该方程的两个实数根,
∴△ABC其余两边的长不相等,
∵△ABC一边的长为5,△ABC是等腰三角形,
∴△ABC的腰长为5,
∴方程x2-(2k-1)x+k2-k-2=0有一个根是5,
∴52-5(2k-1)+k2-k-2=0,
∴k1=4,k2=7,
当k=4时,方程x2-(2k-1)x+k2-k-2=0变形为x2-7x+10=0,该方程的两个实数根是x1=2,x2=5,△ABC的周长是5+5+2=12.
当k=7时,方程x2-(2k-1)x+k2-k-2=0变形为x2-13x+40=0,该方程的两个实数根是x1=8,x2=5,△ABC的周长是5+5+8=18.
∴方程有两个不相等的实数根;
(2)∵方程有两个不相等的实数根,△ABC其余两边的长是该方程的两个实数根,
∴△ABC其余两边的长不相等,
∵△ABC一边的长为5,△ABC是等腰三角形,
∴△ABC的腰长为5,
∴方程x2-(2k-1)x+k2-k-2=0有一个根是5,
∴52-5(2k-1)+k2-k-2=0,
∴k1=4,k2=7,
当k=4时,方程x2-(2k-1)x+k2-k-2=0变形为x2-7x+10=0,该方程的两个实数根是x1=2,x2=5,△ABC的周长是5+5+2=12.
当k=7时,方程x2-(2k-1)x+k2-k-2=0变形为x2-13x+40=0,该方程的两个实数根是x1=8,x2=5,△ABC的周长是5+5+8=18.
点评:本题考查了一元二次方程的解和根的判别式以及等腰三角形性质,关键是根据题意求出△ABC其它两个边的长.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图所示,矩形ABCD的面积为1,E、F分别是AB,BC的中点,试求出△EFC的面积.
如图所示,矩形ABCD的面积为1,E、F分别是AB,BC的中点,试求出△EFC的面积.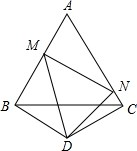 如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由.
如图,△ABC是边长为a的等边三角形,△BCD中,BD=CD,∠BDC=120°,点M,N分别在AB,AC上,且∠MDN=60°.试问:△AMN的周长和面积是否随着点M,N的位置的改变而改变,请说明理由. 如图,抛物线y=ax2+bx+c,则a
如图,抛物线y=ax2+bx+c,则a