题目内容
8. 在大同市开张的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠前,另三边用总长为40m的栅栏围成(如图所示),若设花园的BC长为x(m),花园的面积为y(m2).
在大同市开张的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠前,另三边用总长为40m的栅栏围成(如图所示),若设花园的BC长为x(m),花园的面积为y(m2).(1)求y与x之间的函数关系式,并写出自变量的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x取何值时,花园的面积最大?最大面积为多少?
分析 (1)根据题意可以得到y与x的函数关系式以及x的取值范围;
(2)将y=200代入函数解析式,看x的是否在x的取值范围内,本题得以解决;
(3)将函数解析式化为顶点式,即可得到函数的变化趋势,再结合本题的题意可以得到当x取何值时,花园的面积最大,最大面积是多少.
解答 解:(1)由题意可得,
y=x•$\frac{40-x}{2}$=-$\frac{1}{2}{x}^{2}$+20x(0<x≤15),
即y=-$\frac{1}{2}{x}^{2}$+20x(0<x≤15);
(2)不能,
理由:将y=200代入y=-$\frac{1}{2}{x}^{2}$+20x,
得200=-$\frac{1}{2}{x}^{2}$+20x,
解得,x1=x2=20>15,
∴花园面积不能达到200m2;
(3)∵y=-$\frac{1}{2}{x}^{2}$+20x=$-\frac{1}{2}(x-20)^{2}+200$,
∴函数图象的顶点为(20,200),开口向下,当x<20时,y随x的增大而增大,当x>20时,y随x的增大而减小,
由题意可知,0<x≤15,
∴当x=15时,y最大,此时y=187.5,
即当x取15米时,花园的面积最大,最大面积是187.5m2.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
3.下列是张悦、王强和赵涵的对话,张悦:“从学校向西直走500米,再向北直走100米就到医院了”.王强:“从学校向南直走300米,再向西直走200米就到电影院了.”赵涵:“火车站在电影院正北方向的200米处.”,则医院与火车站相距( )
| A. | 100$\sqrt{3}$米 | B. | 200米 | C. | 300米 | D. | 500米 |
20.下列式之中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{20}$ | C. | $\sqrt{30}$ | D. | $\sqrt{1.5}$ |
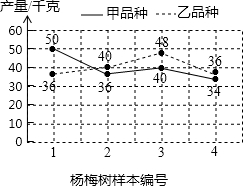 果树改良实验基地育有甲、乙两个品种的杨梅树各100棵,到了收获季,为了分析收成情况,分别从两个品种中随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
果树改良实验基地育有甲、乙两个品种的杨梅树各100棵,到了收获季,为了分析收成情况,分别从两个品种中随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. 操作园地:如图,一副直角三角板△ABC和△DEF,已知BC=DF,∠F=30°,EF=2ED,课堂上,老师将△ABC和△DEF叠加放置像图2的位置,并要求△ABC始终固定不动,将三角板△EDf绕点D逆时针旋转,探究发现图形旋转角与边之间的位置关系.
操作园地:如图,一副直角三角板△ABC和△DEF,已知BC=DF,∠F=30°,EF=2ED,课堂上,老师将△ABC和△DEF叠加放置像图2的位置,并要求△ABC始终固定不动,将三角板△EDf绕点D逆时针旋转,探究发现图形旋转角与边之间的位置关系.