题目内容
9.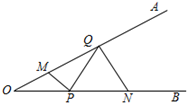 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13.
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13.
分析 首先作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值,易得△ONN′为等边三角形,△OMM′为等边三角形,∠N′OM′=90°,继而求得答案.
解答 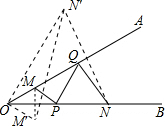 解:作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.
解:作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,OM′=OM=5,ON′=ON=12,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,M′N′=$\sqrt{OM{′}^{2}+ON{′}^{2}}$=13.
故答案为:13.
点评 本题考查了最短路径问题,根据轴对称的定义,找到相等的线段,得到直角三角形是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,把△ABC绕点C按顺时针的方向旋转36°,得到△A'B'C,A'B'交AC于点D,若∠A′DC=90°,则∠A=54°.
如图,把△ABC绕点C按顺时针的方向旋转36°,得到△A'B'C,A'B'交AC于点D,若∠A′DC=90°,则∠A=54°. 如图,已知:梯形ABCD中,AD∥BC,EF过O点且平行于BC,求证:EO=FO.
如图,已知:梯形ABCD中,AD∥BC,EF过O点且平行于BC,求证:EO=FO. 如图,已知△ABC.
如图,已知△ABC.