题目内容
17.解下列方程:(1)x2-2x-3=0
(2)x2-6=6x.
分析 (1)利用因式分解法解方程;
(2)利用配方法解方程.
解答 解:(1)(x-3)(x+1)=0,
x-3=0或x+1=0,
所以x1=3,x2=-1;
(2)x2-6x=6,
x2-6x+9=15,
(x-3)2=15,
x-3=±$\sqrt{15}$,
所以x1=3+$\sqrt{15}$,x2=3-$\sqrt{15}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.若a为方程x2-x-5=0的解,则a-a2+1的值是( )
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
12.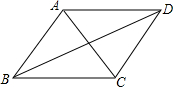 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
如图,下列条件之一能使平行四边形ABCD是菱形的为( )①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ①②③ |
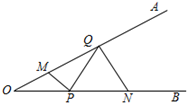 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13.
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13.
 如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的稳定性.
如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的稳定性.