题目内容
13. 如图,已知△ABC.
如图,已知△ABC.(1)用直尺和圆规作出⊙O,使⊙O经过A,C两点,且圆心O在AB边上.(不写作法,保留作图痕迹)
(2)若∠CAB=22.5°,∠B=45°且⊙O的半径为1,试求出AB的长.
分析 (1)利用圆上点的性质作出线段AC的垂直平分线,进而得出答案;
(2)利用线段垂直平分线的性质结合勾股定理得出BO的长,即可得出答案.
解答  解:(1)如图所示:点O即为所求;
解:(1)如图所示:点O即为所求;
(2)由题意可得:MN是AC的垂直平分线,
则AO=CO,
∵∠CAB=22.5°,
∴∠ACO=22.5°,
∴∠COB=45°,
∴∠OCB=90°,CO=BC,
∵⊙O的半径为1,
∴AO=CO=BC=1,
∴BO=$\sqrt{2}$,
∴AB=1+$\sqrt{2}$.
点评 此题主要考查了复杂作图以及勾股定理等知识,正确利用线段垂直平分线的性质得出AO=CO是解题关键.

练习册系列答案
相关题目
17.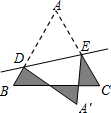 如图,等边△ABC的边长为$\sqrt{3}$cm,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图形的周长为( )cm.
如图,等边△ABC的边长为$\sqrt{3}$cm,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图形的周长为( )cm.
 如图,等边△ABC的边长为$\sqrt{3}$cm,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图形的周长为( )cm.
如图,等边△ABC的边长为$\sqrt{3}$cm,D、E分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在A′处,且A′在△ABC外部,则阴影部分图形的周长为( )cm.| A. | 2$\sqrt{3}$ | B. | $\frac{5}{2}$$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | $\frac{7}{2}$$\sqrt{3}$ |
 . 小新同学计算如下:
. 小新同学计算如下:



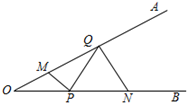 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13.
如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=5,ON=12,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是13. 如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=70°,则∠AOC等于140°.
如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=70°,则∠AOC等于140°. 已知二次函数y=-x2+bx+c的部分图象如图所示,则不等式-x2+bx+c>0的解集是-1<x<3.
已知二次函数y=-x2+bx+c的部分图象如图所示,则不等式-x2+bx+c>0的解集是-1<x<3.