题目内容
15. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,⊙O的切线BP与AC的延长线交于点P,连接DE,BE.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,⊙O的切线BP与AC的延长线交于点P,连接DE,BE.(1)求证:$\widehat{BD}=\widehat{DE}$;
(2)求证:∠AED=∠BCP;
(3)已知:sin∠BAD=$\frac{\sqrt{5}}{5}$,AB=10,求BP的长.
分析 (1)先由直径所对的圆周角是直角得:∠ADB=90°,利用等腰三角形三线合一的性质得出结论;
(2)由四点共圆的性质得:∠DEC=∠ABC,再根据等边对等角证明∠DEC=∠ACB,最后由等角的补角相等可得结论;
(3)先根据已知的三角函数得:BD=2$\sqrt{5}$,三线合一可知:BC=4$\sqrt{5}$,利用勾股定理计算AD=4$\sqrt{5}$,证明△AED∽△BCP,可得:BP=2CP,设CP=x,则BP=2x,在Rt△ABP中,根据勾股定理列方程可得结论.
解答 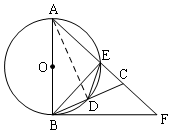 证明:(1)连接AD,
证明:(1)连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴∠BAD=∠CAD,
∴$\widehat{BD}$=$\widehat{DE}$;
(2)∵A、B、D、E四点共圆,
∴∠DEC=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DEC=∠ACB,
∴∠AED=∠BCP;
(3)∵sin∠BAD=$\frac{BD}{AB}=\frac{\sqrt{5}}{5}$,
∴$\frac{BD}{10}=\frac{\sqrt{5}}{5}$,
∴BD=2$\sqrt{5}$,
∴DE=BD=DC=2$\sqrt{5}$,
∴BC=4$\sqrt{5}$,
由勾股定理得:AD=$\sqrt{1{0}^{2}-(2\sqrt{5})^{2}}$=4$\sqrt{5}$,
∵∠DAE=∠BAD=∠PBC,
由(2)得:∠AED=∠BCP;
∴△AED∽△BCP,
∴$\frac{AD}{BP}=\frac{ED}{PC}$,
∴$\frac{4\sqrt{5}}{BP}=\frac{2\sqrt{5}}{PC}$,
∴BP=2CP,
设CP=x,则BP=2x,
在Rt△ABP中,AB2+BP2=AP2,
102+(2x)2=(10+x)2,
解得:x1=0(舍),x2=$\frac{20}{3}$,
∴BP=2x=$\frac{40}{3}$;
则BP的长是$\frac{40}{3}$.
点评 本题考查了切线的性质、四点共圆的性质、解直角三角形、勾股定理、三角形相似的性质和判定以及圆中圆周角、弧的关系,难度适中,熟练掌握圆中圆周角、弧的关系是关键,并与等腰三角形的性质相结合,利用方程的思想求线段的长.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | -2<x<3 | B. | x<3 | C. | x<2 | D. | 无解 |
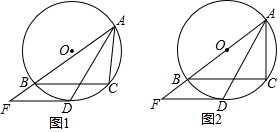
 如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.
如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.