题目内容
13.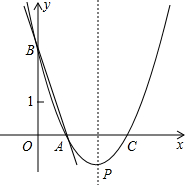 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.求:
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.求:(1)点A、B的坐标;
(2)抛物线的函数表达式;
(3)在抛物线对称轴上是否存在点P,使得以A、B、P为顶点的三角形为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
分析 (1)由y=-3x+3得,当x=0时,y=3;当y=0时,x=1,即可确定点A,B的坐标;
(2)把点A(1,0)、B(0,3)代入y=a(x-2)2+k得:$\left\{\begin{array}{l}{a(1-2)^{2}+k=0}\\{a(0-2)^{2}+k=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$,即可解答;
(3)存在,由AO=1,BO=3,得到AB=$\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$.设对称x轴交于点D,P(2y),D(2,0),所以DA=1,PD=|y|,PA2=PD2+DA2=y2+1,分三种情况讨论解答:当PA=AB即PA2=AB2=10时;当PB=AB即PB2=AB2=10时;当PA=PB即PA2=PB2时.
解答 解:(1)由y=-3x+3得,当x=0时,y=3;当y=0时,x=1
∴A(1,0)、B(0,3).
(2)把点A(1,0)、B(0,3)代入y=a(x-2)2+k得:
$\left\{\begin{array}{l}{a(1-2)^{2}+k=0}\\{a(0-2)^{2}+k=3}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$
∴抛物线的函数表达式为y=(x-2)2-1.
(3)∵AO=1,BO=3,
∴AB=$\sqrt{{3}^{2}+{1}^{2}}=\sqrt{10}$.
设对称x轴交于点D,P(2,y),D(2,0),
∴DA=1,PD=|y|,PA2=PD2+DA2=y2+1,
当PA=AB即PA2=AB2=10时,
∴y2+1=10,
解得y=±3
∴P(2,±3),
但当P(2,-3)时,P、A、B在同一条直线上,不合题意舍去.
∴P1(2,3),
当PB=AB即PB2=AB2=10时,如图,过B作BE⊥对称轴于点E,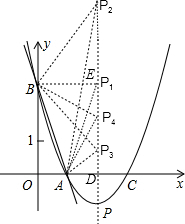
则E(2,3),EB=2,PE2=(y-3)2,
∴PB2=PE2+BE2=(y-3)2+4=10,
解得$y=3±\sqrt{6}$
∴P2(2,3+$\sqrt{6}$)、P3(2,3-$\sqrt{6}$),当PA=PB即PA2=PB2时,
y2+1=(y-3)2+4
解得y=2,
∴P4(2,2).
综上所述,所求的点为P1(2,3),P2(2,3+$\sqrt{6}$),P3(2,3-$\sqrt{6}$),P4(2,2).
点评 本题是二次函数的综合题型,其中涉及到的知识点有二元一次方程组的解法,等腰三角形的性质,勾股定理,二次函数的性质,在(3)中解决问题的关键是采用分类讨论思想解答.

| A. | -1,1 | B. | 2,3 | C. | 3,1 | D. | 1,1 |
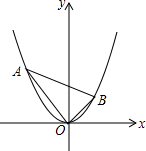 如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )
如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
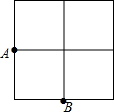 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{7}$ |
| A. | x3与y3 | B. | 3ab2与3a2b | C. | 3与3a | D. | -xy与yx |
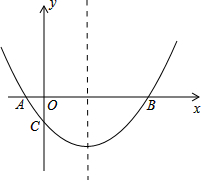 如图,抛物线y=ax2+bx-$\frac{5}{2}$,经过A(-1,0),B(5,0)两点.
如图,抛物线y=ax2+bx-$\frac{5}{2}$,经过A(-1,0),B(5,0)两点.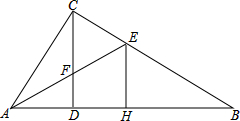 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值.