题目内容
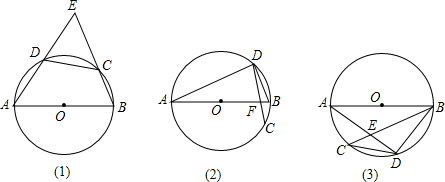
2.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.(1)∠E的度数为600;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
分析 (1)连结OD,OC,BD,根据已知得到△DOC为等边三角形,根据直径所对的圆周角是直角,求出∠E的度数;
(2)同理解答(2)(3).
解答 解:(1)如图1,连结OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°-300=600
∠E的度数为600;
(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°-30°=60°,
(3)如图3,连结OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
点评 本题考查的是圆周角定理及其推论、等边三角形的性质,解题的关键是正确作出辅助线,构造直角三角形,利用直径所对的圆周角是直角进行解答.

练习册系列答案
相关题目
10.“寿岛血脐”是长寿湖的一种新开发的水果,而且是有很高的营养价值,某批发国商第1次共用3.9万元购进A、B两种品牌血脐,全部售完后获得利润6000元,它们的进价如下表:
(1)求该果商第一次购进A、B两种血脐各多少件;
(2)该果商第二次以原价购进A、B两种血脐,购进B种血脐的件数不变,而购进A种血脐的件数是第一次的2倍,A种血脐按原价销售,而B种血脐打折销售,若两种血脐销售完毕,要使得第二次经营活动或利润不少于7500元,求B种血脐最低售价是多少?
| 型 号 | A | B |
| 进价(元/件) | 120 | 100 |
| 售价(元/件) | 135 | 120 |
(2)该果商第二次以原价购进A、B两种血脐,购进B种血脐的件数不变,而购进A种血脐的件数是第一次的2倍,A种血脐按原价销售,而B种血脐打折销售,若两种血脐销售完毕,要使得第二次经营活动或利润不少于7500元,求B种血脐最低售价是多少?
7.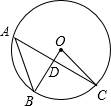 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
 如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )
如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=50°,则∠BOC的度数是( )| A. | 80° | B. | 60° | C. | 50° | D. | 40° |
14.下列说法,正确的是( )
| A. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| B. | -a表示一个负数 | |
| C. | 两个有理数的和一定大于其中每一个加数 | |
| D. | 若-2+x是一个正数,则x一定是正数 |


 如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.
如图是一个正方体的表面展开图,则原正方体中“喜”面所对面上的字是数.