题目内容
9.△ABC中,AB=4,AC=3,若E为BC的中点,且AE=x,x的取值范围为$\frac{1}{2}$<x<$\frac{7}{2}$.分析 连接AE并延长到点F,使AE=EF,连接CF,可证△ABE≌△FCE,可得AB=CF,在△ACF中,根据三角形三边关系即可求得AE的取值范围.
解答 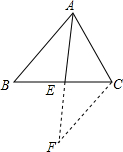 解:连接AE并延长到点F,使AE=EF,连接CF,
解:连接AE并延长到点F,使AE=EF,连接CF,
在△ABE与△FCE中,
∵$\left\{\begin{array}{l}AE=EF\\∠AEB=∠FEC\\ BE=CE\end{array}\right.$,
∴△ABE≌△FCE(SAS).
∵△ACF中,CF-AC<AF<AC+CF,
∴4-3<2AE<3+4,
∴1<2AE<7,
∴$\frac{1}{2}$<AE<$\frac{7}{2}$.
故答案为:$\frac{1}{2}$<x<$\frac{7}{2}$.
点评 本题考查的是三角形的三边关系,熟知三角形两边之和大于第三边,任意两边差小于第三边是解答此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.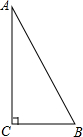 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{13}{3}$ |
14.有一组数据如下:4,a,5,6,8,它们的平均数是6,那么这组数据的方差为( )
| A. | 1 | B. | 2 | C. | 2.5 | D. | 7 |
1.若$\frac{a}{b}$=$\frac{5}{12}$,则$\frac{a-b}{a+b}$的值为( )
| A. | -$\frac{7}{17}$ | B. | $\frac{7}{17}$ | C. | -$\frac{8}{17}$ | D. | $\frac{8}{17}$ |