题目内容
1.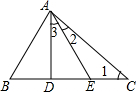 如图,在△ABC中,下列有关说法错误的是( )
如图,在△ABC中,下列有关说法错误的是( )| A. | ∠ADB=∠1+∠2+∠3 | B. | ∠ADE>∠B | C. | ∠AED=∠1+∠2 | D. | ∠AEC<∠B |
分析 根据三角形的外角的性质进行判断即可.
解答 解:由三角形的外角的性质可知,∠ADB=∠3+∠AED,∠AED=∠1+∠2,
∴∠ADB=∠1+∠2+∠3,A正确;
∵∠ADE是△ABD的外角,
∴∠ADE>∠B,B正确;
由三角形的外角的性质可知,∠AED=∠1+∠2,C正确;
∠AEC>∠B,D错误,
故选:D.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列说法正确的是( )
| A. | 4$\sqrt{3}$-2$\sqrt{3}$=2 | B. | 方程3x2+27=0的解是x=±3 | ||
| C. | 等弧所对的圆周角相等 | D. | 等边三角形是中心对称图形 |
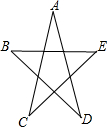 如图,则∠A+∠B+∠C+∠D+∠E的度数是180°.
如图,则∠A+∠B+∠C+∠D+∠E的度数是180°.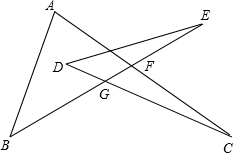 如图,求∠A+∠B+∠C+∠D+∠E的度数.
如图,求∠A+∠B+∠C+∠D+∠E的度数. 如图,已知DC是∠ACB的外角平分线,∠BAC与∠1的大小关系如何?∠BAC与∠2呢?∠2与∠B呢?∠BAC与∠B呢?
如图,已知DC是∠ACB的外角平分线,∠BAC与∠1的大小关系如何?∠BAC与∠2呢?∠2与∠B呢?∠BAC与∠B呢?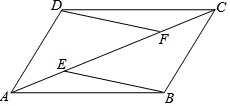 已知:如图,AD∥BC,AD=BC,E、F是四边形ABCD的对角线AC上的两点,并且AE=CF,
已知:如图,AD∥BC,AD=BC,E、F是四边形ABCD的对角线AC上的两点,并且AE=CF,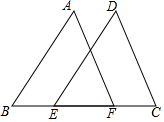 如图,已知点E、F在BC上,且BE=CF,AB=CD,∠B=∠C,试说明△ABF≌△DCE.
如图,已知点E、F在BC上,且BE=CF,AB=CD,∠B=∠C,试说明△ABF≌△DCE.