题目内容

13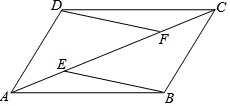．已知：如图，AD∥BC，AD=BC，E、F是四边形ABCD的对角线AC上的两点，并且AE=CF，
（1）求证：△AFD≌△CEB； 
（2）试判断EB与DF的位置关系．

分析 （1）根据SAS即可判定△AFD≌△CEB；
（2）利用全等三角形的性质即可判定．

解答 （1）证明：∵AD∥BC，
∴∠DAF=∠BCE，
∵AE=CF，
∴AF=CE，
在△DAF和△BCE中，
$\left\{\begin{array}{l}{AD=BC}\\{∠DAF=∠BCE}\\{AF=CE}\end{array}\right.$，
∴△AFD≌△CEB．

（2）结论：EB=DF．
理由：∵△AFD≌△CEB，
∴EB=DF．

点评 本题考查全等三角形的判定和性质，解题的关键是熟练掌握全等三角形的判定和性质，属于基础题，中考常考题型．

练习册系列答案
相关题目
11．由四舍五入得到的近似数2.6万，精确到（　　）
A．千位B．万位C．个位D．十分位
4．（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D．
（2）阅读下面的内容，并解决后面的问题：
如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC=36°，∠ADC=16°，求∠P的度数．
解：∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2，∠3=∠4
由（1）的结论得：$\left\{\begin{array}{l}{∠P+∠3=∠1+∠B①}\\{∠P+∠2=∠4+∠D②}\end{array}\right.$
①+②，得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P=$\frac{1}{2}$（∠B+∠D）=26°．
①如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
②在图4中，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．
③在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论，无需说明理由．
1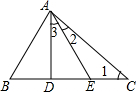．如图，在△ABC中，下列有关说法错误的是（　　）
A．∠ADB=∠1+∠2+∠3B．∠ADE＞∠BC．∠AED=∠1+∠2D．∠AEC＜∠B
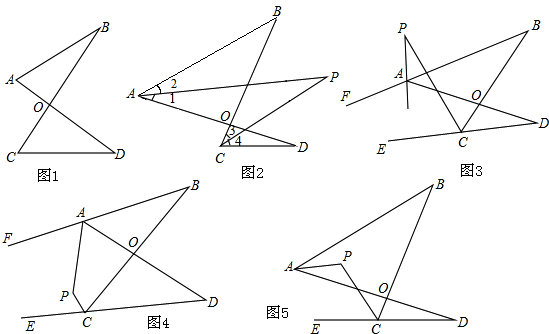
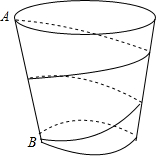8．如图，一只杯子的上下底面分别是直径为5cm和7.5cm的圆，母线AB的长为15cm．
（1）求杯子的侧面积．
（2）从点B出发，绕着杯子两圈画一条装饰线，终点为A，求装饰线的最短长度．
18．已知在Rt△ABC中，AC=BC，∠C=90°，D为边AB的中点，∠EDF=90°，∠EDF绕点D旋转，它的两边分别交AC、CB（或它们的延长线）于点E、F．
（1）当∠EDF绕点D旋转到DE⊥AC于点E时（如图（1）），易证S△DEF+S△CEF=$\frac{1}{2}$S△ABC．
（2）当∠EDF绕点D旋转到DE和AC不垂直时，在图（2）和图（3）这两种情况下，上述结论是否成立？若成立，请给予说明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需说明．
5．下列5个说法：
①两个形状相同的图形称为全等图形；
②两个圆是全等图形；
③两个正方形是全等图形；
④全等图形的形状和大小都相同；
⑤面积相等的两个三角形是全等图形．
其中，说法正确的是④．
2．计算：
①（-3）×（-9）-8×（-5）；
②-63÷7+45÷（-9）；
③-3×22-（-3×2）3；        
④（-0.1）3-$\frac{1}{4}$×（-$\frac{3}{5}$）2；
⑤-23-3×（-2）3-（-1）4；      
⑥（$\frac{1}{2}$-$\frac{5}{9}$+$\frac{5}{6}$-$\frac{7}{12}$）×（-36）；
⑦[11×2-|3÷3|-（-3）2-33]÷$\frac{3}{4}$； 
⑧（-1）3-（1-$\frac{1}{2}$）÷3×[2-（-3）2]．
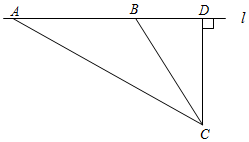3．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道l上确定点D，使CD与l垂直，测得CD的长等于24米，在l上点D的同侧取点A、B，使∠CAD=30°，∠CBD=60°．
（1）求AB的长（结果保留根号）；
（2）已知本路段对校车限速为45千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网