Question

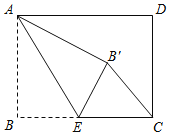
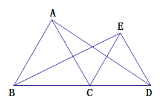
【题目】如图，点C为线段BD上的一点，△ABC和△CDE是等边三角形.

（1）求证：AD=BE.

（2）以点C为中心，将△CDE逆时针方向旋转，旋转角为ɑ(0°＜ɑ＜360°).

①当ɑ为多少时DE∥AB?直接写出结果，不要求证明.

②当BC=6, CD=4时 ,设点E到直线AB的距离为y, 当ɑ为多少时，点E到直线AB的距离最小？求出最小值，并简洁说明理由.

Answer 1

【答案】（1）证明见解析；（2）120°或300°；（3）,,证明见解析.

【解析】

（1）利用SAS证明△BCE≌△ACD，从而得到结论；

（2）①分两种情况：当CE旋转到与CB重合时，DE∥AB；当CE旋转到BC延长线上时，DE∥AB，从而进行分析即可；

②当点E旋转到AB边上的高线上时，到直线AB的距离最小，利用勾股定理可求出，再利用三角形三边关系及垂线段性质即可证明.

（1）证明：∵△ABC和△CDE是等边三角形，

∴BC=AC,CE=CD,∠BCA=∠ECD=60°，

∴∠BCA+∠ACE=∠ECD+∠ACE，即∠BCE=∠ACD，

∴△BCE≌△ACD（SAS）

∴AD=BE；

（2）解：①情况一：当 时，DE∥AB，证明如下：

当 时，此时CE旋转到与CB重合，

∵△ABC和△CDE是等边三角形，

∴∠DEC=∠ABC=60°，

∴DE∥AB（同位角相等，两直线平行）；

情况二：当 时，DE∥AB，证明如下：

当 时，此时CE旋转到BC延长线上，

∵△ABC和△CDE是等边三角形，

∴∠DEC=∠ABC=60°，

∴DE∥AB（内错角相等，两直线平行）；

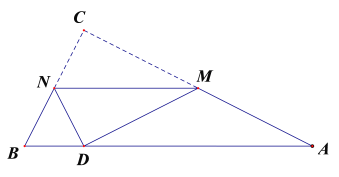
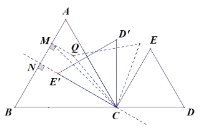
②如图，当时，点E旋转至点E'，此时点E'到AB的距离最短，NC⊥AB，

在Rt△ANC中，AC=6，AN=，

∴NC=，

∴，

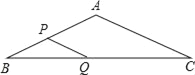
如图，Q为E旋转任意角度后所对应的点，根据三角形三边关系可知，CQ+QMMC，

根据垂线段最短可知，CE'+NE'MCCQ+QM，当点Q与点E'重合时取等号，即：NE'≤QM，

所以当时，点E到直线AB的距离最小，最小值为.