题目内容
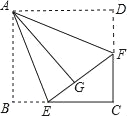
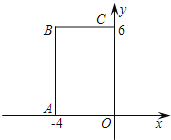
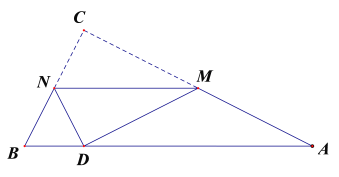
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后,顶点
翻折后,顶点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,已知
处,已知![]() ,则四边形
,则四边形![]() 的面积是__________
的面积是__________
【答案】![]()
【解析】
根据折叠全等可得∠CMN=∠DMN,CM=MD,又根据平行可得∠CMN=∠A,∠NMD=∠MDA,等量代换得到∠MDA=∠A,MD=MA=CM,同理可得CN=BN=ND,即可得出MN为三角形ABC的中位线,易证△CNM∽△CBA,可以得出两个三角形的相似比,即可得出两个三角形的面积比,根据题意可求出△CNM的面积,然后求出△CBA的面积,两个面积相减即可求出四边形![]() 的面积.
的面积.
∵将![]() 沿直线
沿直线![]() 翻折后,顶点
翻折后,顶点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,
处,
∴△CMN≌△DMN,
∴∠CMN=∠DMN,CM=MD,
∵![]() ,
,
∴∠CMN=∠A,∠NMD=∠MDA
∴∠MDA=∠A,
∴MD=MA=CM;
同理可得:CN=BN=ND,
∴M、N分别为CA、CB中点,
∴![]() ,
,
∵![]() ,
,
∴△CNM∽△CBA,
∵![]() ,
,
∴两个三角形的相似比为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目