Question

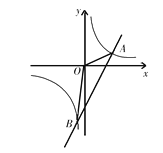
【题目】如图，平行于x轴的直线AC分别交抛物线与于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则DE：BC=______.

Answer 1

【答案】

【解析】

设A点坐标为（0，a），利用两个函数解析式求出点B、C的坐标，然后求出BC的长度，再根据CD∥y轴，利用y1的解析式求出D点的坐标，然后利用y2求出点E的坐标，从而得到DE的长度，然后求出比值即可得解．

解：如图，

设A点坐标为（0，a），（a＞0），
则x2=a，解得x=，

∴点B（，a），

∵，

则x=，

∴点C（，a），

∴BC=．

∵CD∥y轴，

∴点D的横坐标与点C的横坐标相同，为，

∴y1=（）2=3a，

∴点D的坐标为（，3a）．

∵DE∥AC，

∴点E的纵坐标为3a，

∴，

∴，

∴点E的坐标为：（），

∴DE=，

∴；

故答案为：.