题目内容
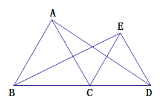
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 是
是![]() 中点,点
中点,点![]() 为边
为边![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为边在
为边在![]() 的左侧作等边三角形
的左侧作等边三角形![]() ,连接
,连接![]() .
.
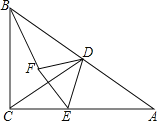
(1)![]() 的形状为______;
的形状为______;
(2)随着点![]() 位置的变化,
位置的变化,![]() 的度数是否变化?并结合图说明你的理由;
的度数是否变化?并结合图说明你的理由;
(3)当点![]() 落在边
落在边![]() 上时,若
上时,若![]() ,请直接写出
,请直接写出![]() 的长.
的长.
【答案】(1)等边三角形;(2)![]() 的度数不变,理由见解析;(3)2
的度数不变,理由见解析;(3)2
【解析】
(1)由![]() 、
、![]() ,可得出
,可得出![]() 、
、![]() ,结合点
,结合点![]() 是
是![]() 中点,可得出
中点,可得出![]() ,进而即可得出
,进而即可得出![]() 为等边三角形;
为等边三角形;
(2)由(1)可得出![]() ,根据
,根据![]() 可得出
可得出![]() ,再结合
,再结合![]() 、
、![]() 即可得出
即可得出![]() ,根据全等三角形的性质即可得出
,根据全等三角形的性质即可得出![]() ,即
,即![]() 的度数不变;
的度数不变;
(3)易证![]() 为等腰三角形,由等腰三角形及等边三角形的性质可得出
为等腰三角形,由等腰三角形及等边三角形的性质可得出![]() ,进而可得出
,进而可得出![]() .
.
解:(1)∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() 为等边三角形.
为等边三角形.
故答案为:等边三角形.
(2)![]() 的度数不变,理由如下:
的度数不变,理由如下:
∵![]() ,点
,点![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∴![]() .
.
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
又∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
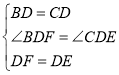 ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 的度数不变.
的度数不变.
(3)∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰三角形,
为等腰三角形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目