题目内容
15. 我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).(1)若水箱的底面积为16000cm2,请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)
分析 (1)设切去的小正方形的边长为xcm,然后用含x的式子表示水箱底面的长和宽,然后依据矩形的面积公式列方程求解即可;
(2)依据正方体的体积=底面积×高求得水的体积,然后再依据1升水=1000cm3水求解即可.
解答 解:(1)设切去的小正方形的边长为xcm.
根据题意,得:(280-2x)(160-2x)=16000,
化简整理,得:x2-220x+7200=0,
解得x=40或x=180(舍去).
答:切去的小正方形边长为40cm.
(2)在(1)的条件下,水箱的容积=16000×40=640000cm3.
640000÷1000=640(升)
答:这时水量为640升.
点评 本题主要考查的是一元二次方程的应用,用含x的式子表示水箱底面的长和宽是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1. 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )| A. | (-2,1) | B. | (-1,2) | C. | ($\sqrt{3}$,-1) | D. | (-$\sqrt{3}$,1) |
3.已知△ABC的三边长分别是5cm,12cm,13cm,则△ABC的面积是( )
| A. | 30cm2 | B. | 78cm2 | C. | $\frac{65}{2}$cm2 | D. | 60cm2 |
10. 如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是( )
如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是( )
 如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是( )
如图,△ABC是等腰直角三角形,点D是斜边AB上一点,DE⊥AC于点E,DF⊥BC于点F,AC=4,则EF的最小值是( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
 已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
已知△ABC中,∠A=90°,AB=AC,D为BC的中点. 如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
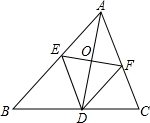 如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.
如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.