Question

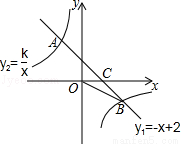
如图，一次函数y1=﹣x+2的图象与反比例函数y2=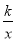的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC=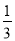，点B的坐标为（m，n）．

（1）求反比例函数的解析式；

（2）请直接写出当x＜m时，y2的取值范围．

Answer 1

（1）反比例函数解析式为y2=-；（2）当0＜x＜4时，y2的取值范围是y2＜-2，当x＜0时，y2＞0．

【解析】

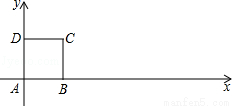
试题分析：（1）作BD⊥x轴于D，如图，在Rt△OBD中，根据正切的定义得到tan∠BOC=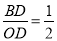，则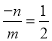，即m=-2n，再把点B（m，n）代入y1=-x+2得n=-m+2，然后解关于m、n的方程组得到n=-2，m=4，即B点坐标为（4，-2），再把B（4，-2）代入y2=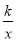可计算出k=-8，所以反比例函数解析式为y2=-；

（2）观察函数图象得到当x＜4，y2的取值范围为y2＞0或y2＜-2．

试题解析：（1）作BD⊥x轴于D，如图，

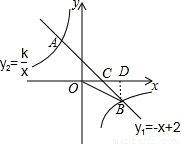
在Rt△OBD中，tan∠BOC=，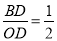

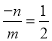∴，即m=-2n，

把点B（m，n）代入y1=-x+2得n=-m+2，

∴n=2n+2，解得n=-2，

∴m=4，

∴B点坐标为（4，-2），

把B（4，-2）代入y2=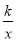得k=4×（-2）=-8，

∴反比例函数解析式为y2=-

（2）当0＜x＜4时，y2的取值范围是y2＜-2，当x＜0时，y2＞0．

考点：反比例函数与一次函数的交点问题．