题目内容
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.
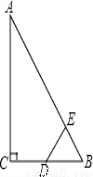
t的值为2或3.5或4.5.
【解析】
试题分析:由Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,可求得AB的长,由D为BC的中点,可求得BD的长,然后分别从若∠DEB=90°与若∠EDB=90°时,去分析求解即可求得答案.
试题解析:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=2BC=4(cm),
∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发,
∴BD= BC=1(cm),BE=AB-AE=4-t(cm),
BC=1(cm),BE=AB-AE=4-t(cm),
若∠BED=90°,
当A→B时,∵∠ABC=60°,
∴∠BDE=30°,
∴BE= BD=
BD= (cm),
(cm),
∴t=3.5,
当B→A时,t=4+0.5=4.5.
若∠BDE=90°时,
当A→B时,∵∠ABC=60°,
∴∠BED=30°,
∴BE=2BD=2(cm),
∴t=4-2=2,
当B→A时,t=4+2=6(舍去).
综上可得:t的值为2或3.5或4.5.
考点:1.相似三角形的判定与性质;2.含30度角的直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

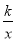 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=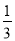 ,点B的坐标为(m,n).
,点B的坐标为(m,n).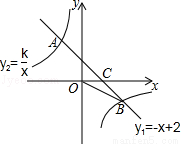
 (x>0)的图像与△ABC有公共点,则k的取值范围是( )
(x>0)的图像与△ABC有公共点,则k的取值范围是( )
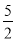 C.2 D.
C.2 D.

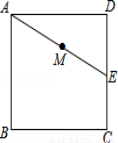
 米的某学生想测量学校旗杆的高度,当他站在
米的某学生想测量学校旗杆的高度,当他站在 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是( )
处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是( )
 米 B.7米 C.8米 D.9米
米 B.7米 C.8米 D.9米 