题目内容
二次函数y=-x2-3x+c上有两点A(2,y1),B(-4,y2),则y1,y2的大小关系为( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法确定 |
考点:二次函数图象上点的坐标特征
专题:
分析:根据二次函数图象上点的坐标特征,分别求出y1,y2,即可得解.
解答:解:y1=-22-3×2+c=-10+c,
y2=-(-4)2-3×(-4)+c=-4+c,
∵-10+c-(-4+c)=-6,
∴y1<y2.
故选B.
y2=-(-4)2-3×(-4)+c=-4+c,
∵-10+c-(-4+c)=-6,
∴y1<y2.
故选B.
点评:本题考查了二次函数图象上点的坐标特征,表示出y1,y2是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
为了检查一批零件的长度,从中取50个进行检测,在这个问题中个体是( )
| A、零件长度的全体 |
| B、50 |
| C、50个零件 |
| D、每个零件的长度 |
已知二次函数y=kx2-2x+1与一次函数y=k(x-1)-
的图象对于任意的非零实数k都有公共点,则k的取值范围是( )
| k |
| 4 |
| A、-1≤k≤1且k≠0 |
| B、-1≤k≤1 |
| C、k≤-1或k≥1 |
| D、任意实数 |
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为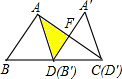 如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为
如图,在Rt△ABC中,AB=3,BC=5,∠BAC=90°,D是斜边BC的中点,将△ABD沿BC方向移动,使得点B与点D恰好重合,得到△A′B′D′,A′B′与AC相交于点F,则图中阴影部分(△ADF)的面积为 如图,O为矩形ABCD的中心(AB<BC),过O且互相垂直的两条直线被矩形四边所截,设截得的线段EF和GH长度分别为x,y,四边形EGFH的面积为S,当这两条直线保持垂直且围绕O点不停旋转时,下列说法正确的是( )
如图,O为矩形ABCD的中心(AB<BC),过O且互相垂直的两条直线被矩形四边所截,设截得的线段EF和GH长度分别为x,y,四边形EGFH的面积为S,当这两条直线保持垂直且围绕O点不停旋转时,下列说法正确的是( )