题目内容
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=22.5°,CD=6,则扇形BOC的面积为考点:扇形面积的计算,垂径定理,圆周角定理
专题:
分析:由圆周角定理知∠COE的度数,然后通过解直角三角形求得线段OC,然后利用扇形的面积公式求解.
解答: 解:∠BOC=2∠CDB=45°,
解:∠BOC=2∠CDB=45°,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=
CD=3,
∴OC=3
,
则扇形BOC的面积为:
=
.
故答案是:
.
 解:∠BOC=2∠CDB=45°,
解:∠BOC=2∠CDB=45°,∵AB是⊙O的直径,弦CD⊥AB,
∴CE=
| 1 |
| 2 |
∴OC=3
| 2 |
则扇形BOC的面积为:
45π×(3
| ||
| 360 |
| 9π |
| 4 |
故答案是:
| 9π |
| 4 |
点评:本题考查了垂径定理、扇形面积的计算,通过解直角三角形得到相关线段的长度是解答本题的关键.

练习册系列答案
相关题目
二次函数y=-x2-3x+c上有两点A(2,y1),B(-4,y2),则y1,y2的大小关系为( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法确定 |
 如图,已知直线l:y=
如图,已知直线l:y= 如图,AB切⊙O于点A,BO交⊙O于点C,点D是优弧
如图,AB切⊙O于点A,BO交⊙O于点C,点D是优弧
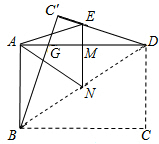 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为 小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示
小明骑自行车从家出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局沿一条道路步行回家,小明在邮局停留2分钟后沿原理以原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD、线段EF分别是表示