题目内容
在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑”.如记
=1+2+3+…+(n-1)+n,
(x+k)=(x+3)+(x+4)+…+(x+n);已知
[(x+k)(x-k+1)]=5x2+5x+m,则m的值是( )
| ||
| k-1 |
| ||
| k-3 |
| ||
| k-2 |
| A、40 | B、-70 |
| C、-40 | D、-20 |
考点:平方差公式
专题:新定义
分析:根据题中的新定义将已知等式左边化简,再利用多项式相等的条件即可确定出m的值.
解答:解:根据题意得:
[(x+k)(x-k+1)]
=(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)+(x+6)(x-5)
=5x2+5x+m,
整理得:5x2+5x-70=5x2+5x+m,
则m=-70.
故选B.
| ||
| k-2 |
=(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)+(x+6)(x-5)
=5x2+5x+m,
整理得:5x2+5x-70=5x2+5x+m,
则m=-70.
故选B.
点评:此题考查了平方差公式,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
下列计算错误的是( )
| A、-15+20=5 | ||||
B、
| ||||
C、4
| ||||
| D、-3-8=-11 |
二次函数y=-x2-3x+c上有两点A(2,y1),B(-4,y2),则y1,y2的大小关系为( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法确定 |
根据阿里巴巴集团公布的消息称,从11•11购物狂欢节正式开启,截至11•11日24点,淘宝网11•11购物节支付宝总销售额达到191亿元,创造了中国零售新纪录,请用科学记数表示191亿元为( )
| A、1.91×1011元 |
| B、1.91×1010元 |
| C、1.91×109元 |
| D、1.91×1012元 |
定义新运算“*”:对于任意两个实数a、b,有a*b=b2-1,例如:6*4=42-1=15.那么当m为实数时,m*(m*
)=( )
| 2013 |
| A、20132-1 |
| B、20122-1 |
| C、20112-1 |
| D、m2-1 |

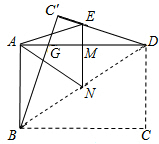 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,则EM的长为
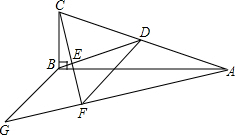 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过A作BD的平行线,交CE的延长线与点F,在AF的延长线上截取FG=BD,连接BG,DF.若AF=8,CF=6,则四边形BDFG的周长为多少?
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过A作BD的平行线,交CE的延长线与点F,在AF的延长线上截取FG=BD,连接BG,DF.若AF=8,CF=6,则四边形BDFG的周长为多少?