Question

4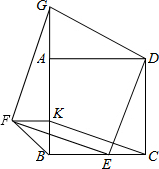．如图，四边形ABCD是正方形，点E、K分别在DC、AB上，CE=BK，点G在BA的延长线上，DG⊥DE．
（1）证明：DE=DG；
（2）以线段DE、DG为边作正方形DEFG，连接KF、BF．证明：S_{四边形CEFK}=2S_△BFK．（S_{四边形CEFK}、S_△BFK分别为四边形CEFK、△BFK的面积）

Answer 1

分析 （1）由四边形ABCD是正方形，DG⊥DE，易证得△ADG≌△CDE，然后由全等三角形的性质，证得：DE=DG；
（2）由CE=BK，易证得△KBC≌△ECD，又由以线段DE、DG为边作正方形DEFG，证得CK∥EF，CK=EF，即可证得四边形CEFK是平行四边形，继而证得结论．

解答 证明：（1）∵四边形ABCD是正方形，
∴DA=DC，∠DAB=∠ADC=∠DCE=90°，
∴∠DAG=90°，∠CDE+∠ADE=90°，
∵DG⊥DE，
∴∠ADE+∠ADG=90°，
∴∠ADG=∠CDE，
在△ADG和△CDE中，
$\left\{\begin{array}{l}{∠ADG=∠CDE}\\{DA=DC}\\{∠DAG=∠DCE}\end{array}\right.$，
∴△ADG≌△CDE（ASA），
∴DE=DG；

（2）设DE与CK交于点O，
∵四边形ABCD是正方形，
∴∠KBC=∠ECD=90°，BC=CD，
在△KBC和△ECD中
$\left\{\begin{array}{l}{BC=CD}\\{∠KBC=∠ECD}\\{KB=EC}\end{array}\right.$，
∴△KBC≌△ECD（SAS），
∴DE=CK，∠DEC=∠BKC，
∵∠ABC=90°，
∴∠KCB+∠BKC=90°，
∴∠KCB+∠DEC=90°，
∴∠EOC=180°-90°=90°，
∵四边形DEFG是正方形，
∴EF=DE，∠FED=90°=∠EOC，
∴CK=EF，CK∥EF，
∴四边形CEFK是平行四边形，
∴BK⊥FK，
∴S_{四边形CEFK}=FK•BK，S_△BFK=$\frac{1}{2}$FK•BK，
∴S_{四边形CEFK}=2S_△BFK．

点评 此题考查了正方形的性质、全等三角形的判定与性质以及平行四边形的性质与判定．注意证得△ADG≌△CDE，△KBC≌△ECD以及四边形CEFK是平行四边形是解此题的关键．