题目内容
16.已知x+y=6,xy=4,x>y,则$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$=$\frac{\sqrt{5}}{5}$.分析 根据x+y=6,xy=4,x>y,可以求得x-y的值,从而可以解答本题.
解答 解:∵x+y=6,xy=4,x>y,
∴x-y=$\sqrt{(x+y)^{2}-4xy}=\sqrt{{6}^{2}-4×4}=2\sqrt{5}$,
∴$\frac{\sqrt{x}-\sqrt{y}}{\sqrt{x}+\sqrt{y}}$
=$\frac{x-2\sqrt{xy}+y}{x-y}$
=$\frac{(x+y)-2\sqrt{xy}}{x-y}$
=$\frac{6-2\sqrt{4}}{2\sqrt{5}}$
=$\frac{\sqrt{5}}{5}$,
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7. 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )| A. | 7.8米 | B. | 3.2米 | C. | 2.3米 | D. | 1.5米 |
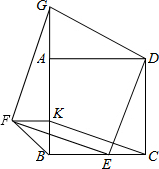 如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.
如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE. 如图,已知在梯形ABCD中,AB∥CD,∠1=∠2,试说明EF∥GH的理由.
如图,已知在梯形ABCD中,AB∥CD,∠1=∠2,试说明EF∥GH的理由.